07.01.2024r
Inercjalny i nieinercjalny układ odniesienia. Siły bezwładności
Spis treści- Układ odniesienia – skąd to się wzięło? (Ł)
- Siły rzeczywiste i siły pozorne (bezwładności) (Ł)
- Siła dośrodkowa i siła odśrodkowa (Ś)
- Siła Coriolisa (Ś)
- Czy układ odniesienia może być jednocześnie inercjalny i nieinercjalny? (Ł)
- Szybki teścik
Wskazywanie na potrzeby rozwiązywania zadań i problemów mechaniki układów odniesienia, a już w szczególności nazywanie ich „inercjalnymi” lub „nieinercjalnymi” może być przytłaczające. Przyzwyczajeni jesteśmy od najmłodszych lat do potocznego opisywania ruchu, tym bardziej opis naukowy zdaje się nam niepraktyczny. Gdy policjant zatrzymuje nas za zbyt szybką jazdę samochodem, nie dopytujemy go względem jakiego układu odniesienia zmierzył naszą prędkość. Tłumaczymy się jedynie z czego wynika nasz pośpiech wiedząc, że co do złamania przepisu ma po prostu rację.
Układ odniesienia – skąd to się wzięło?
 Rys. 1. Mechanika podczas jazdy samochodem [1]. Siła ciągu generowana przez silnik przekłada się na przyspieszenie względem ziemi. Odnosząc się jednak do samochodu przed nami lub pasażera obok, będziemy mieli odpowiednio przyspieszenie ujemne lub zerowe.
Rys. 1. Mechanika podczas jazdy samochodem [1]. Siła ciągu generowana przez silnik przekłada się na przyspieszenie względem ziemi. Odnosząc się jednak do samochodu przed nami lub pasażera obok, będziemy mieli odpowiednio przyspieszenie ujemne lub zerowe.
Układ inercjalny to taki, w którym obowiązują prawa Newtona.
Załóżmy, że zarówno my jak i auto przed nami poruszamy się jednostajnie, czyli ze stałą prędkością względem ziemi, np. 100 km/h. Wtedy gdy my przyspieszymy do prędkości 120 km/h dzięki przyłożeniu siły F, to przyspieszyliśmy o 20 km/h zarówno względem jezdni jak i względem drugiego samochodu! Przyspieszenie a = F/m jest prawdziwe dla obu rozważanych układach odniesienia, dlatego można powiedzieć:
Układem inercjalnym jest każdy układ nie poruszający się, lub poruszający się jednostajnie prostoliniowo względem innego układu inercjalnego.
Wszystkie pozostałe układy odniesienia są nieinercjalne co oznacza, że nie można w nich wprost zastosować zasad dynamiki Newtona. Możemy też powiedzieć, że poruszają się z przyspieszeniem względem dowolnego układu inercjalnego. Czy to oznaczy, że prawa Newtona nie obowiązują?! Zauważmy, że siły grawitacji, oporu, elektryczne i wszystkie pozostałe nie zależą od układu odniesienia. Grawitacja między dwoma ciałami jest zawsze taka sama! Mówiąc, że w układzie nieinercjalnym nie obowiązują zasady dynamiki mamy po prostu na myśli, że skutek tych sił w postaci obserwowanego ruchu będzie inny, niż wynikałoby to z zasad Newtona (siła (ciągu silnika) działa, a samochód nie porusza się (względem czegoś) itp.).
Siły rzeczywiste i siły pozorne (bezwładności)
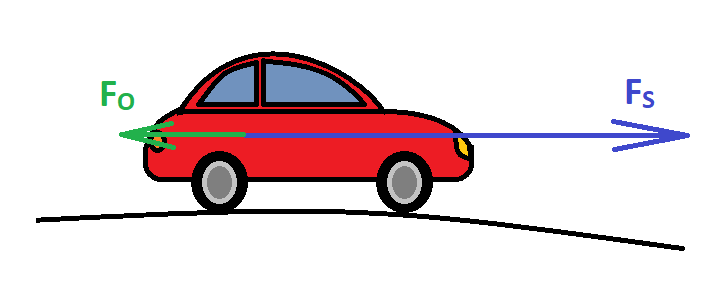 Rys. 2. Z punktu widzenia układu inercjalnego, samochód przyspiesza, gdyż siła ciągu silnika przewyższa siły oporu. Kierowca stwierdzi jednak, że względem własnego pojazdu w ogóle się nie porusza. Jak to możliwe?
Rys. 2. Z punktu widzenia układu inercjalnego, samochód przyspiesza, gdyż siła ciągu silnika przewyższa siły oporu. Kierowca stwierdzi jednak, że względem własnego pojazdu w ogóle się nie porusza. Jak to możliwe?
$${ a = \frac{F_{W} }{ m } = \frac{8\,000 }{ 2\,000 } = 4 \frac{m}{s^{2}} }$$
Kierowca odnosząc się do drogi lub budynków za szybą rzeczywiście obserwuje swoje przyspieszenie. Siła ciągu silnika i oporów powietrza całkowicie wyjaśniają więc ten ruch. Gdy kierowca porówna się jednak do swojego samochodu (nieinercjalny układ odniesienia) to stwierdzi, że w ogóle nie przemieszcza się, a przyspieszenie jest zerowe. Spróbujmy więc wyjaśnić to zjawisko dostosowując niejako równanie Newtona do tej obserwacji.
$${ a_{2} = \frac{F_{W2} }{ m } }$$
Obserwujemy, że nasze przyspieszenie wynosi 0:
$${ a_{2} = 0 = \frac{F_{W2} }{ m } }$$
Jak wcześniej policzyliśmy, działa siła silnika i siła oporu, których suma nie wynosi jednak 0. Postulujemy więc dodanie dodatkowego czynnika, siły składowej o symbolu Fb:
$${ 0 = \frac{F_{s} – F_{o} + F_{b} }{ m } }$$
Którą można wyznaczyć jako:
$${ F_{b} = - \frac{F_{s} – F_{o} }{ m } \cdot m = - a \cdot m \tag{1} }$$
Ta dodatkowa siła to siła bezwładności. Jest nazywana siłą pozorną, gdyż nie można wskazać jej źródła i nie występuje w układzie inercjalnym. Dla układu nieinercjalnego jest z kolei niezbędna, aby uspójnić opis ruchu z układem inercjalnym. Pozorność nie oznacza jednak, że jest tylko matematyczną zagrywką. Siła bezwładności występuje w opisie dla układu nieinercjalnego, i również dla obserwatora związanego z tym układem jest jak najbardziej odczuwalna. Siedząc za kierownicą samochodu jesteśmy związani z pojazdem, a więc z układem nieinercjalnym. Czujemy, jak jakaś dodatkowa siła wpycha nas w fotel, odczuwamy więc siłę bezwładności.
Siły bezwładności występują dla każdego układu nieinercjalnego i umożliwiają opis ruchu w tym układzie z wykorzystaniem praw Newtona. Poza omówioną siłą bezwładności w ruchu postępowym, spotykamy się też z siłą odśrodkową oraz siłą Coriolisa.
Siła dośrodkowa i siła odśrodkowa
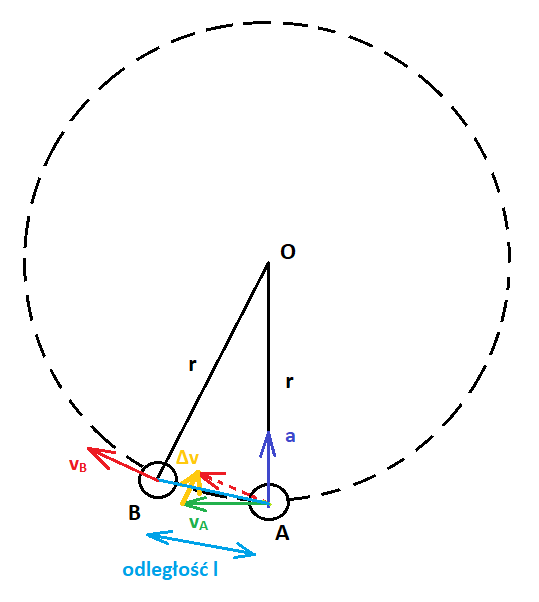 Rys. 3. Zmiana kierunku ruchu ciężarka wynika z działania przyspieszenia dośrodkowego, a więc prostopadłego do chwilowego wektora prędkości.
Rys. 3. Zmiana kierunku ruchu ciężarka wynika z działania przyspieszenia dośrodkowego, a więc prostopadłego do chwilowego wektora prędkości.
$${ \Delta v = v_{A} \cdot \frac{l}{r} = {v_{A}}^{2} \cdot \frac{ \Delta t }{ r} }$$
Teraz możemy skorzystać z ogólnego wzoru na przyspieszenie:
$${ a = \frac{\Delta v }{ \Delta t} }$$
$${ a = \frac{{v_{A}}^2 \Delta t }{ r \Delta t} = \frac{{v_{A}}^2 }{ r} }$$
Właśnie to przyspieszenie jest odpowiedzialne za zakrzywianie toru ruchu ciężarka (czy też Księżyca). Działa w takim samym kierunku jak zaobserwowana zmiana prędkości Δv, a więc do osi obrotu.
Zgodnie z II Zasadą Dynamiki Newtona z przyspieszeniem zawsze związana jest siła. Wynosi ona:
$${ F = ma = \frac{mv^{2} }{ r} \tag{2} }$$
Jest to siła dośrodkowa. Jest ona siłą rzeczywistą i zawsze możemy wskazać konkretne jej źródło. W przypadku Księżyca siłą dośrodkową jest siła grawitacji – GMm/r^2. W przypadku ciężarka – siłą ciągu sznurka. W przypadku elektronu krążącego na orbicie jądra atomowego – siła elektrostatyczna.
Powyższy opis ruchu wykonaliśmy z perspektywy układu inercjalnego. Obserwowaliśmy ruch „z boku”. Teraz wyobraźmy sobie, że jesteśmy muchą, która usiadła na obracającym się ciężarku – rys. 4.
a)
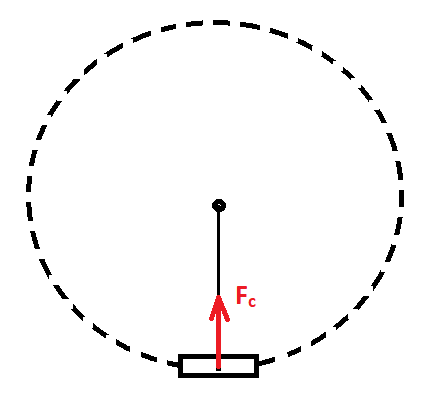
b)
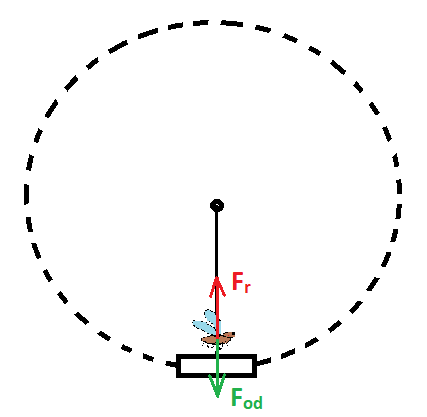
Siła Coriolisa
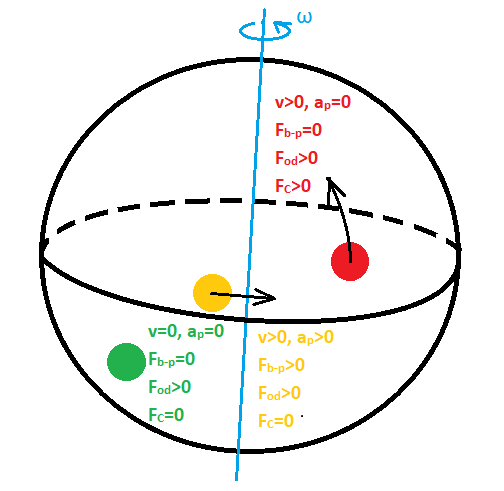 Rys. 5. Siły pozorne w układzie nieinercjalnym. Ciało zielone nie porusza się względem ziemi, więc działa na nie jedynie siła odśrodkowa. Ciało żółte przemieszcza się z przyspieszeniem a, więc działa na nie siła bezwładności Fb-p=-am, jednak porusza się wzdłuż równika, więc nie działa na nie siła Coriolisa (stała odległość od osi obrotu). Ciało czerwone przemieszcza się przecinając równoleżniki, zmienia odległość od osi obrotu Ziemi, a więc działa na nie siła Coriolisa.
Rys. 5. Siły pozorne w układzie nieinercjalnym. Ciało zielone nie porusza się względem ziemi, więc działa na nie jedynie siła odśrodkowa. Ciało żółte przemieszcza się z przyspieszeniem a, więc działa na nie siła bezwładności Fb-p=-am, jednak porusza się wzdłuż równika, więc nie działa na nie siła Coriolisa (stała odległość od osi obrotu). Ciało czerwone przemieszcza się przecinając równoleżniki, zmienia odległość od osi obrotu Ziemi, a więc działa na nie siła Coriolisa.
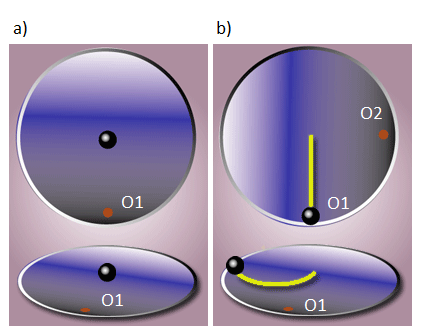 Rys. 6. Piłka poruszająca się po obracającej się tarczy [2].Górne grafiki przedstawiają obserwację ruchu z inercjalnego układu odniesienia, dolne – z nieinercjalnego. Obrazki pochodzą z wikipedii i tam też można obejrzeć animację.
Rys. 6. Piłka poruszająca się po obracającej się tarczy [2].Górne grafiki przedstawiają obserwację ruchu z inercjalnego układu odniesienia, dolne – z nieinercjalnego. Obrazki pochodzą z wikipedii i tam też można obejrzeć animację.
$${ a = \frac{d^{2} x }{ dt^{2} } = \frac{ d(d(\omega v_{p} t^{2})) }{ d(dt) } = \frac{ d( 2 \omega v_{p} t) }{ dt } = 2 \omega v_{p} }$$
Na koniec możemy stwierdzić, że zgodnie z II Zasadą Dynamiki Newtona z przyspieszeniem tym związana jest siła:
$${ F = am = 2m \omega v_{p} }$$
Otrzymaliśmy wzór na siłę Coriolisa, którą możemy zaobserwować obok siły bezwładności w ruchu postępowym i siły odśrodkowej. Zazwyczaj podaje się ją w bardziej ogólnej postaci wektorowej:
$${ \vec{F} = 2m\, \vec{v} \times \vec{\omega} \tag{4}}$$
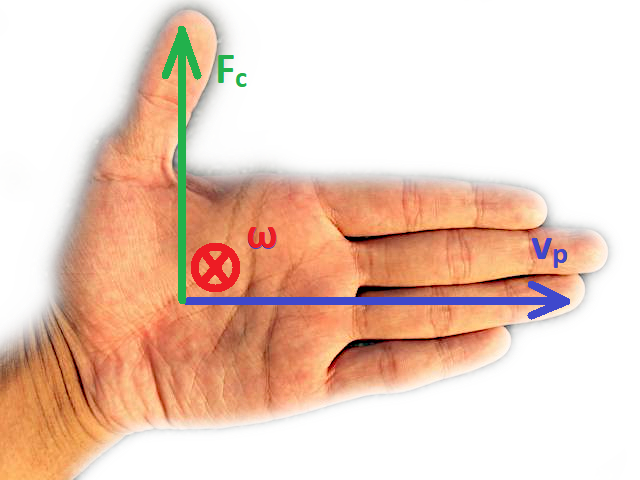
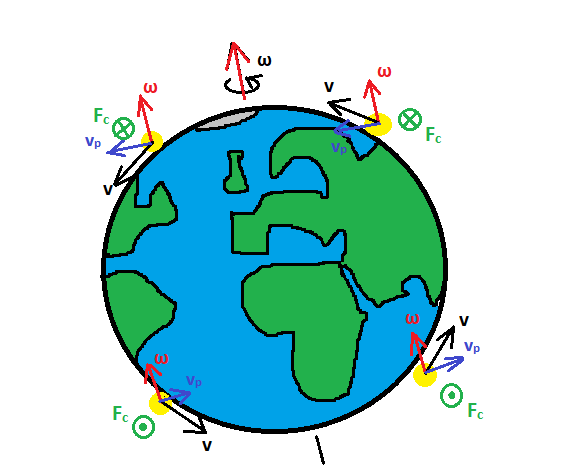
Widzimy w nim iloczyn wektorowy prędkości v oraz prędkości kątowej ω. Zapis ten jest bardzo ważny – pokazuje, że nie każdy kierunek przemieszczanie się ciała w układzie wirującym powoduje pojawienie się siły Coriolisa! Mówiąc precyzyjniej, ciało musi się zbliżać lub oddalać od osi obrotu. Z tego powodu np. przemieszczanie się ciała po równiku Ziemi nie powoduje powstanie tej siły, ale już jazda na północ lub południe tak, gdyż zbliżamy się lub oddalamy od osi obrotu Ziemi. Kierunek zaś działania siły również wynika z iloczynu wektorowego – możemy go ustalić stosując metodę lewej dłoni – rys. 7a. Kierunek działania siły Coriolisa na ciała przemieszczające się na naszej planecie pokazane zostały dodatkowo na rys. 7b.
a)
b)
Czy układ odniesienia może być jednocześnie inercjalny i nieinercjalny?
W naszym życiu codziennym powierzchnia ziemi stanowi układ inercjalny. Można powiedzieć, że względem poruszającego się samochodu czy zawieszonego na suficie wahadła ziemia jest nieruchoma. Jeżeli jednak spojrzymy na naszą planetę z przestrzeni kosmicznej, np. lecąc rakietą na Marsa, to szybko stwierdzimy, że nie jest ona dobrym, stałym punkt odniesienia. Zauważymy, że nie dość, że Ziemia obraca się wokół własnej osi, to jeszcze porusza się po elipsie wokół Słońca. Nasza rakieta nie będzie się poruszała ruchem jednostajnym prostoliniowym względem Błękitnej planety, nawet jeśli wyłączymy silniki. Jako inercjalny układ odniesienia wygodnie będzie przyjąć wtedy Słońce. Z drugiej strony rakieta po wyłączeniu silników stanie się dobrym inercjalnym układem odniesienia dla satelity geostacjonarnej lub Księżyca. Z perspektywy kosmonauty na tę satelitę działa siła grawitacji Ziemi, która powoduje jej ciągłe „spadanie”, czyli krążenie po orbicie. Pracownik znajdujący się na satelicie powie jednak, że nie przemieszcza się względem swojej kosmicznej kajuty – będzie on odczuwał dodatkową siłę, siłę odśrodkową, równoważącą grawitację Ziemi. Te przykłady skłaniają do zadania pytania, czy istnieje uniwersalny układ odniesienia, który pozostaje zawsze inercjalny? Pytanie to jest bardziej skomplikowane niż mogłoby się wydawać. Przestrzeń kosmiczna sama w sobie nieustannie „puchnie”, a wszystkie obiekty kosmiczne odsuwają się od siebie. Jak na razie ludzie nie zdołali jednak znacząco oddalić się od powierzchni własnej planety, a pokonywane odległości są niewielkie w porównaniu do całego Wszechświata. Wskazanie więc lokalnie stałego punktu odniesienia (w skali kosmicznej) jest wystarczające i całkiem łatwe 😊Szybki teścik
Bibliografia
- Wykorzystano grafiki z serwisu Pexels, https://www.pexels.com, dostęp: 07.01.2024
- Efekt Coriolisa, https://pl.wikipedia.org/wiki/Efekt_Coriolisa, dostęp: 07.01.2024

