09.12.2022r

Współrzędne kartezjańskie i biegunowe w fizyce

Spis treści
  1. Opis położenia piłki w układzie kartezjańskim (Ł)
  2. Kartezjański a biegunowy układ odniesienia (Ś)
  3. Ruch po okręgu we współrzędnych biegunowych i kartezjańskich (Ś)
  4. Rzut ukośny we współrzędnych biegunowych (Ś)
  5. Inne układy współrzędnych w fizyce (Ś)
  6. Szybki teścik

Znaczną część zjawisk fizycznych opisuje się w oderwaniu od położenia ciał. Jest tak gdy rozważamy zmiany temperatury obiektu w czasie, natężenia i napięcia prądu w obwodzie czy aktywność promieniotwórczą próbki izotopu. Gdy jednak chcemy określić położenie obiektu, musimy posłużyć się układem odniesienia (kubek stoi 10 cm od brzegu biurka, jabłko wisi 2 m nad ziemią itp.). W formalnym opisie zjawisk układ odniesienia opisujemy najczęściej korzystając ze współrzędnych kartezjańskich. Czasem jednak wygodniej jest zastosować współrzędne biegunowe, sferyczne czy walcowe.

Opis położenia piłki w układzie kartezjańskim

Z układem kartezjańskim mamy styczność od wczesnych lat edukacji. Na matematyce pojawia się układ współrzędnych x i y, a w przypadku obiektów trójwymiarowych x, y i z. Również w życiu codziennym, często nieświadomie, opisujemy położenie ciała poprzez prostopadłe do siebie osie – rys. 1.
uklad kartezjanski wspolrzedne zycie codzienne
Rys. 1. Układ kartezjański stosujemy intuicyjnie – łatwo przychodzi nam rozłożenie cech obiektu na prostopadłe do siebie kierunki x i y.
Również w fizyce jest to najczęściej stosowany układ współrzędnych. Rozważmy rzut ukośny opisany w tym temacie.

Chłopiec rzuca piłkę „pod skosem do góry”. Naszym zadaniem jest wyznaczenie położenia piłki w kolejnych sekundach ruchu. Ruch ten opiszemy w układzie kartezjańskim, a więc rozłożymy go na osie x i y, jak na rysunku 2.

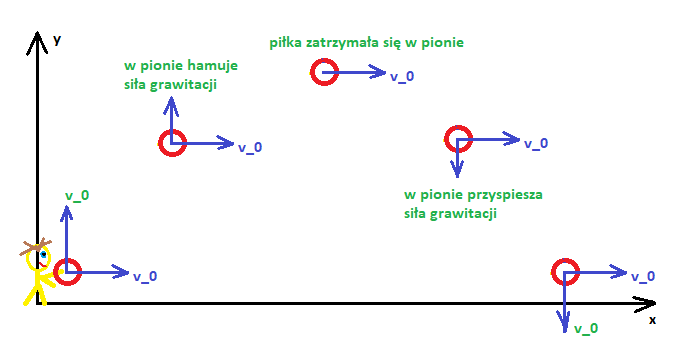rzut ukosny kartezjanski Rys. 2. Rzut ukośny opisany w kartezjańskim układzie współrzędnych.
Przyjmijmy za początek układu współrzędnych punkt, w którym stoi człowiek. Jest to punkt (0, 0). Piłka znajduje się w pewnej odległości od obu osi, załóżmy, że jest to odległość 1 m. Możemy więc powiedzieć, że początkowe położenie piłki wynosi:
(1, 1)
Dodatkowo przyjmijmy, że nadaliśmy piłce prędkość 5 m/s w obu kierunkach, to jest zarówno wzdłuż osi x i y. Wzdłuż osi poziomej piłka porusza się ruchem jednostajnym. Jej położenie początkowe to 1. Korzystając więc ze wzoru na drogę pokonywaną w ruchu jednostajnym możemy opisać położenie piłki: $${ x(t) = x_{0} + v_{0x} t = 1 + 5t }$$ Wzdłuż osi pionowej ciało przemieszcza się ruchem jednostajnie opóźnionym. Możemy więc napisać:
$${ y(t) = y_{0} + v_{0y} t – \frac{1}{2} a t^{2} = 1 + 5t – \frac{1}{2} 10 t^{2} = 1 + 5t – 5t^{2} }$$
Uzyskaliśmy w ten sposób dwa wzory zależne jedynie od czasu. Możemy więc przepisać je jako formuły w programie Excel i wyliczyć położenia piłki w kolejnych sekundach ruchu, a następnie wykreślić wykresy obrazujące ruch – rysunek 3.
polozenie pilka uklad kartezjanski
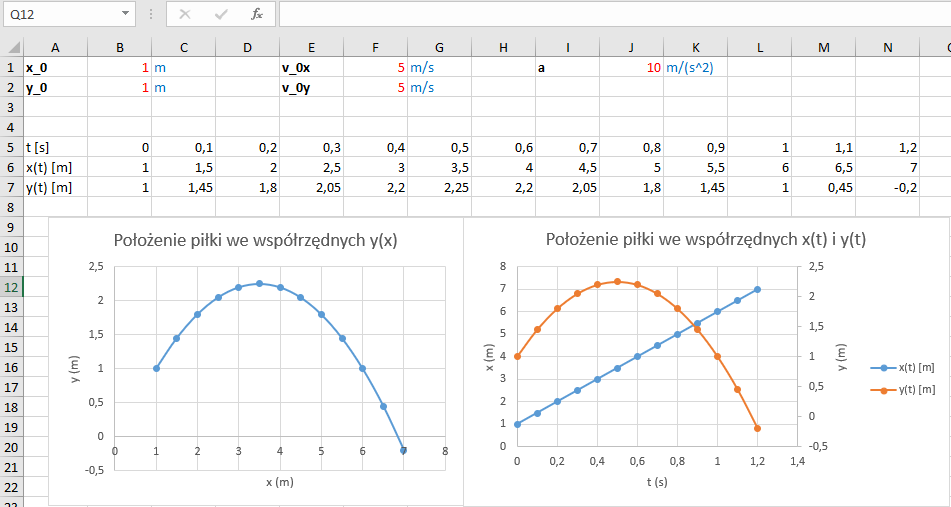
Rys. 3. Położenie piłki w kartezjańskim układzie współrzędnych
Dobrze sporządzone wykresy ułatwiają wyciągnięcie wniosków na temat przemieszczania się ciała. W naszym przypadku można powiedzieć, że piłka wzniesie się na maksymalną wysokość ok 2,2 m, po czym spadnie na ziemię po niespełna 1,2 s. W tym czasie pokona odległość niespełna 6 mw kierunku poziomym - równolegle do ziemi.

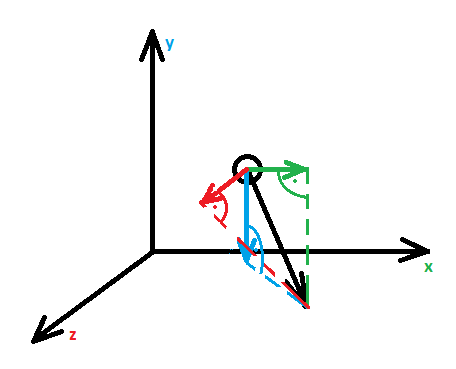uklad kartezjanski wektor Rys. 4. Rozkład wielkości wektorowej na trzy składowe w kartezjańskim układzie współrzędnych.
Czasem, w przypadku zjawisk zachodzących w trzech wymiarach, kartezjański układ współrzędnych uzupełnia się o trzecią oś z – rysunek 4.

Kartezjański a biegunowy układ odniesienia

Innym przykładem układu współrzędnych jest układ biegunowy. Jest on bardzo wygodny do opisu ruchu po okręgu. W tym przypadku punkt (położenie) jest opisane nie przez współrzędne x i y, ale przez promień r i kąt skierowany φ – rysunek 5.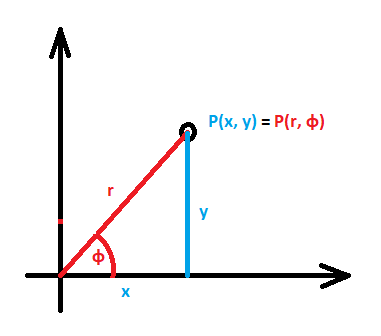
wspolrzedne biegunowe kartezjanskie zamiana Rys. 5. Współrzędne kartezjańskie oraz biegunowe. Zauważmy, że oba rodzaje opisu położenia jednoznacznie określają punkt w przestrzeni.


Co ważne, zarówno podanie współrzędnych x i y, jak i podanie promienia r i kąta φ, jednoznacznie wyznaczają punkt w przestrzeni. Innymi słowy nie ma dwóch położeń o tych samych współrzędnych. Analizując rysunek 5, dojdziemy również do łatwej metody zamiany jednego sposobu opisu na drugi. Wystarczy zauważyć, że podane współrzędne utworzyły trójkąt prostokątny. Jeżeli mamy więc punkt opisany poprzez współrzędne r i φ, to x i y wyglądają następująco: $${ x = r ~cos(\phi) \tag{1} }$$ $${ y = r ~sin(\phi) \tag{2} }$$ Z kolei jeśli mamy współrzędne x i y, to r i φ otrzymamy następująco: $${ r = \sqrt{x^{2} + y^{2}} \tag{3} }$$ $${ tg (\phi) = \frac{y}{x} ~~~ => ~~~ \phi = arctg(\frac{y}{x}) \tag{4} }$$
uklad biegunowy wspolrzedne zycie codzienne Rys. 6. Stosowanie współrzędnych biegunowych w życiu codziennym również jest możliwe, ale raczej mało praktyczne.
Skoro opis w obu układach współrzędnych jest jednoznaczny i równorzędny, to również położenie Franka w oknie bloku z rysunku 1 można podać we współrzędnych biegunowych – rysunek 6. Jest to jednak rozwiązanie nie wygodne i często mniej precyzyjne.

Ruch po okręgu we współrzędnych biegunowych i kartezjańskich

Wyobraźmy sobie następujący przykład – na sznurku o długości 1,2 m zawieszamy ciężarek, po czym zaczynamy kręcić tak, aby linka cały czas była naprężona. Ciężarek wykonuje 2 obroty na sekundę. Opiszmy położenie ciężarka w biegunowym układzie współrzędnych, przyjmując miejsce zawieszenia sznurka (rękę trzymającą sznurek) za początek układu – rys. 7.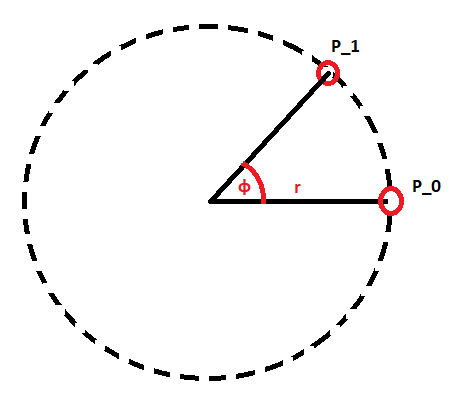

ruch po okregu uklad biegunowy Rys. 7. Opis ruchu po okręgu w biegunowym układzie współrzędnych.
Promień okręgu, po którym przemieszcza się ciężarek jest stały w czasie i równy długości sznurka - wynosi 1,2 m. Prędkość kątowa wynika z liczby wykonywanych obrotów w jednostce czasu i wynosi: $${ \omega = \frac{\phi}{t} = \frac{2 \cdot 360^{o} }{1~s} = 720 \frac{ 1}{s} }$$ Możemy więc zapisać współrzędne biegunowe ciężarka. Pamiętajmy przy tym, że pokonywany kąt zależy od prędkości kątowej podobnie, jak pokonywana droga zależy od prędkości w ruchu postępowym: $${ r (t) = r_{0} = 1,2 ~ m }$$ $${ \phi (t) = \phi_{0} + \omega t = 720 t }$$

Ten sam ruch możemy opisać również w układzie kartezjańskim – rys. 8.
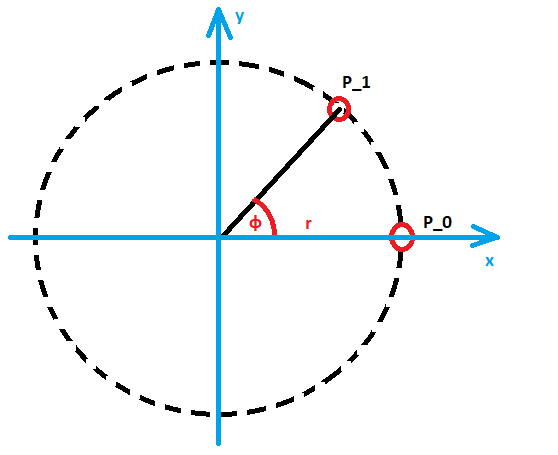ruch po okregu uklad kartezjanski Rys. 8. Opis ruchu po okręgu w kartezjańskim układzie współrzędnych.
W tym celu skorzystamy z zależności 1 i 2 służących do zamiany układu współrzędnych: $${ x (t) = r(t) \cdot ~cos(~\phi(t)~) = 1,2 ~cos(720 t) ~m }$$ $${ y (t) = r(t) \cdot ~sin(~\phi(t)~) = 1,2 ~sin(720 t) ~m }$$
Na koniec tego ćwiczenia porównajmy wykresy współrzędnych biegunowych i kartezjańskich od czasu w programie Excel – rys. 9.
wspolrzedne biegunowe kartezjanskie ruch po okregu
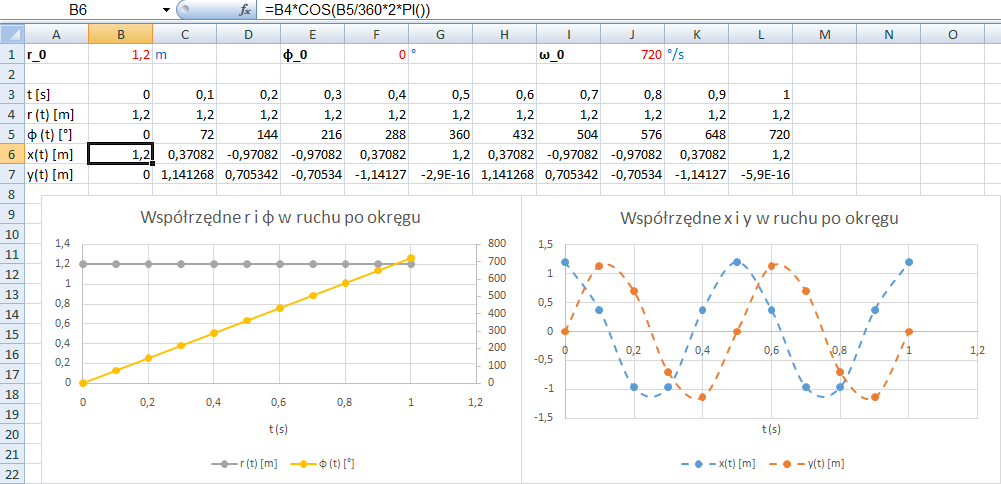
Rys. 9. Opis położenia ciężarka zawieszonego na sznurku we współrzędnych biegunowych i kartezjańskich.
Wykresami współrzędnych biegunowych są linie proste, z kolei kartezjańskich – sinusoidy. To pokazuje siłę współrzędnych biegunowych - opis zjawiska przebiegającego „kołowo” (np. ruch ciała po okręgu) jest prostszy niż dla współrzędnych kartezjańskich.

Rzut ukośny we współrzędnych biegunowych

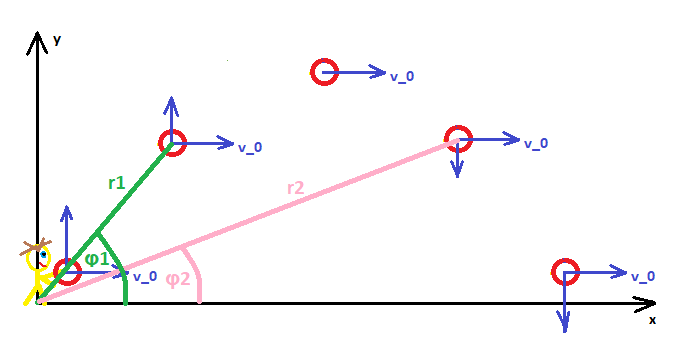rzut ukosny biegunowy kartezjanski Rys. 10. Rzut ukośny opisany we współrzędnych biegunowych.
Jako ostatnie ćwiczenie, spróbujmy wyrazić jeszcze współrzędne kartezjańskie poprzez biegunowe w przykładzie z rzutem ukośnym – rys. 10. W tym celu wykorzystamy wyznaczone wcześniej wzory na współrzędne x i y: $${ x(t) = 1 + 5t }$$ $${ y(t) = 1 + 5t – 5t^{2} }$$ podstawiamy zależności do wzorów 3 i 4:
$${ r(t) = \sqrt { x(t)^{2} + y(t)^{2} }= \sqrt{ ( 1+5t)^{2} + (1 + 5t – 5t^{2})^{2} } }$$
$${ tg (\phi) = \frac{y(t)}{x(t)} ~~~~ => ~~~~ \phi = arctg(\frac{y(t)}{x(t)}) = arctg (\frac{1 + 5t – 5t^{2} }{ 1 + 5t} ) }$$

Otrzymane zależności wyglądają na skomplikowane. Nie będziemy ich upraszczać, za to przeniesiemy je jako formuły do programu Excel. Przepisujemy równania i wykreślamy wykresy – rys. 11.
polozenie pilka uklad kartezjanski biegunowy
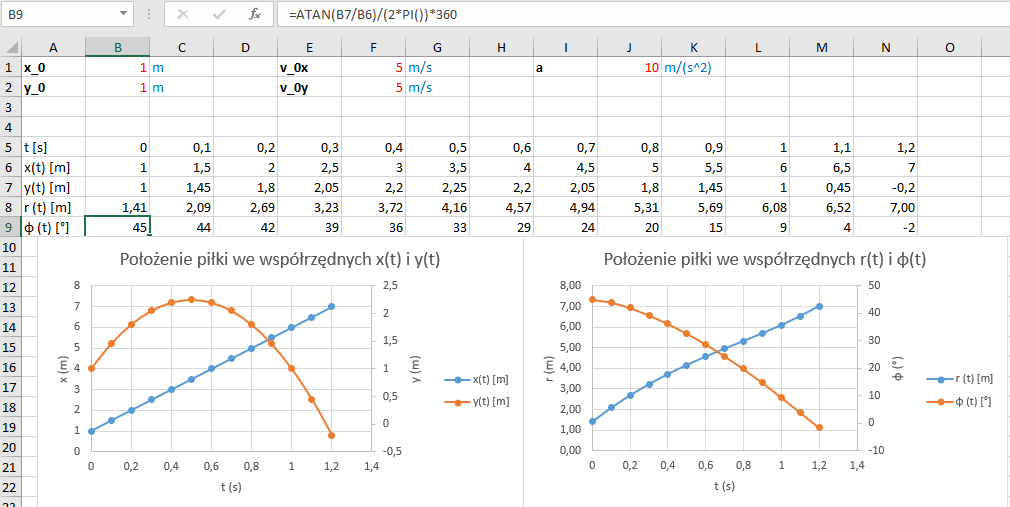
Rys. 11. Porównanie wykresów opisujących rzut ukośny we współrzędnych kartezjańskich i biegunowych.

Opis rzutu ukośnego w układzie kartezjańskim jest dosyć prosty – sprowadza się do funkcji liniowej dla współrzędnej x i funkcji kwadratowej (paraboli) dla współrzędnej y. W przypadku układu biegunowego, obie współrzędne są wyrażone poprzez złożone, trudne do analizy funkcje matematyczne. Jest to opis niepraktyczny, co nie zmienia faktu, że jest poprawny.

Inne układy współrzędnych w fizyce

Oprócz układu kartezjańskiego i biegunowego w fizyce spotyka się również inne metody opisu położenia ciał. Wśród nich warto wymienić współrzędne sferyczne, które stanowią rozszerzenie współrzędnych biegunowych o trzeci wymiar, czy współrzędne walcowe operujące promieniem, wysokością i kątem. Zgrabny opis zamiany zmiennych z układu kartezjańskiego na sferyczne czy walcowe można znaleźć na przykład pod tym linkiem [1].

Do opisu położenia w przestrzeni możemy posłużyć się również dowolnym innym systemem, jaki tylko przyjdzie nam do głowy! Warunkiem koniecznym do spełnienia jest jednak to, aby nasz układ współrzędnych określał położenie w sposób jednoznaczny.

Szybki teścik

Układ kartezjański i biegunowy:
Zamiana zmiennych ze współrzędnych kartezjańskich na biegunowe odbywa się w oparciu o:
Uogólnieniem współrzędnych biegunowych do trzech wymiarów są:

Bibliografia

  1. Zamiana zmiennych, https://pg.edu.pl/files/cnm/2021-03/Zamiana_Zmiennych.pdf, dostęp: 08.12.2022

Komentarze