23.11.2022r
Cewki elektryczne
Spis treści- Pętla z prądem (Ś)
- Solenoid, cewka elektryczna (Ś)
- Cewka elektryczna – prawo Ampere’a (T)
- Cewka Helmholtza (Ś)
- Gradientowa cewka Maxwella (Ś)
- Tłumienie pola magnetycznego tła, aktywny ekran (Ś)
- Szybki teścik
Odkąd technika elektryczna zaczęła rozwijać się naprawdę dynamicznie, a więc już w XIX wieku, cewki stały się jednym z podstawowych budulców najróżniejszych maszyn. Znaleziono dla nich wiele, czasem bardzo różniących się, zastosowań. Co przysporzyło im aż takiej popularności? Z punktu widzenia fizyki kluczowe dla XIX – wiecznych odkryć było sformułowanie teorii elektromagnetyzmu - od powiązania zjawiska elektryczności i magnetyzmu w postaci siły Lorentza począwszy, aż po sformułowanie równań Maxwella stanowiących pewien rodzaj „biblii” elektromagnetyzmu. Cewka jest świetnym przykładem, jak pole elektryczne i magnetyczne ze sobą „współpracują” dając nam użyteczne i bardzo proste narzędzie.
Rys. 1. Przykłady cewek (zwojnic, solenoidów) [1].
Pętla z prądem
Rys. 2. Pętle z prądem. Dobrym modelem cewki jest szeregowe połączenie pojedynczych pętli z prądem.
Rozważania na temat pola magnetycznego cewki rozpoczniemy od obliczenia pola magnetycznego pojedynczej pętli wykorzystując prawo Biota-Savarta. Pole magnetyczne całej cewki można by otrzymać poprzez dodanie do siebie pól poszczególnych pętli. W tym celu trzeba by ustalić liczbę zwojów oraz ich rozstaw. Niestety, takie obliczenia są trudne do wykonania „na papierze”, dlatego w drugim kroku wykonamy symulację pola tą metodą w programie excel – obliczenia numeryczne często z dużą dokładnością umożliwiają zastąpienie trudnych rachunkowo wzorów.
Analityczne rozwiązanie dla pola cewki można łatwo otrzymać stosując prawo Ampere’a. Takie rozważanie również pokazane zostanie w dalszej części tematu.
Rozpocznijmy więc od pola pojedynczej pętli z prądem. Prawo Biota-Savarta ma postać: $${ \Delta \vec B = \frac{\mu_{0}}{4\pi} \frac {I \Delta \vec l \times \vec r} {r^3} \tag{1} }$$ Lub w postaci różniczkowej: $${ d \vec B = \frac{\mu_{0}}{4\pi} \frac {I d \vec l \times \vec r} {r^3} \tag{2} }$$ Prawo to umożliwia policzenie pola magnetycznego od przewodników nawet o skomplikowanym kształcie, na co nie zawsze pozwala prawo Ampere’a. Sprowadza się ono do podziału przewodnika na nieskończenie małe fragmenty, policzenia pól przez nie generowanych, a następnie ich zsumowaniu. Należy zwrócić szczególną uwagę na iloczyn wektorowy fragmentu przewodnika dl oraz wektora wodzącego r, który występuje w liczniku wzoru i determinuje kierunek i zwrot pola magnetycznego.
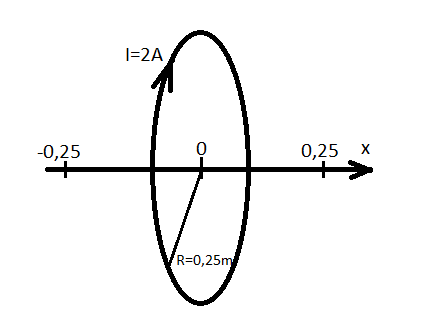
Najłatwiej zrozumieć prawo Biota-Savarta na przykładzie, dlatego od razu przejdźmy do obliczenia pola przewodnika kołowego – rysunek 3. We wzorach zawrzemy jedynie wartość pola. Kierunek wektorów ustalimy korzystając z reguły lewej dłoni.
Rys. 3. Zastosowanie prawa Biota-Savarta do obliczenia indukcji pola magnetycznego pętli z prądem.
Obliczamy pole magnetyczne w dowolnym punkcie położonym na osi pętli. Przewodnik z prądem dzielimy na małe fragmenty o długości Δl. Korzystając z reguły lewej dłoni wyznaczamy kierunek pola ΔB. Zauważmy, że pole ΔB możemy rozłożyć na składową poziomą i pionową. Zwróćmy uwagę na bardzo istotny fakt – składowe pionowe dla przewodników przeciwległych Δl i Δl_2 wzajemnie się znoszą. Nasze zadanie sprowadza się więc do policzenia składowej poziomej.
Drugą ważną obserwacją jest to, że wektory Δl oraz r są prostopadłe. Wartość ich iloczynu wektorowego wynosi więc: $${ \Delta \vec l \times \vec r = \Delta l r sin(\alpha) = \Delta l r sin(90^o) = \Delta l r }$$
Powyższe obserwacje pozwalają uprościć wzór na pole magnetyczne: $${ \Delta \vec B = \frac{\mu_{0}}{4\pi} \frac {I \Delta \vec l \times \vec r} {r^3} = \frac{\mu_{0}}{4\pi} \frac {I \Delta l} {r^2} }$$ Składową poziomą zaś tego pola otrzymamy stosując funkcję trygonometryczną: $${ \Delta B_x = \Delta B sin(\alpha) = \Delta B \frac {R}{r} = \frac{\mu_{0}}{4\pi} \frac {I R \Delta l } {r^3} }$$ Ile wynosi więc całkowite pole magnetyczne pętli z prądem? Wystarczy zsumować wkład do pola od poszczególnych fragmentów: $${ B_{x} = \sum{ \Delta B_{x} } = \sum{ \frac{\mu_{0}}{4\pi} \frac {I R \Delta l} {r^3}} }$$ A ponieważ czynnik $${ \frac{\mu_{0}}{4\pi} \frac {I R} {r^3} }$$ jest taki sam dla każdego Δl, to możemy zapisać: $${ B_x = \frac{\mu_{0}}{4\pi} \frac {I R} {r^3} \sum{ \Delta l } }$$ Dodanie do siebie czynników Δl daje długość całego okręgu: $${ B_x = \frac{\mu_{0}}{4\pi} \frac {I R} {r^3} 2\pi R= \frac{\mu_{0}}{2\pi} \frac {I \pi R ^{2}} {r^3} \tag{3} }$$ W ten sposób otrzymaliśmy wzór na pole magnetyczne pętli z prądem w dowolnym punkcie na osi. Wzór ten znacznie uprości się, jeśli zapytamy jedynie o punkt w samym środku pętli. Wtedy r = R: $${ B_x = \frac{\mu_{0}}{2\pi} \frac {I \pi R ^{2}} {R^3} = \frac{\mu_{0}I }{2R } \tag{4} }$$ Obliczenia z zachowaniem pełnego formalizmu matematycznego przyjęły by postać różniczkową. Pomijając początkowe, identyczne przekształcenia wzorów, zapiszmy wartość pola dB_x: $${ d B_x = \frac{\mu_{0}}{4\pi} \frac {I R d l } {r^3} }$$ następnie sumowanie zastępujemy operatorem całki: $${ \int_0^{B_x} { d B_x } = \int_{0}^{2\pi R} \frac{\mu_{0}}{4\pi} \frac {I R} {r^3} dl }$$ $${ B_x = \frac{\mu_{0}}{4\pi} \frac {I R} {r^3} \int_0^{2\pi R} dl }$$ Całka z dl to l: $${ B_x = \frac{\mu_{0}}{4\pi} \frac {I R} {r^3} [ l ]_{0}^{2 \pi R} }$$ Otrzymujemy identyczny wynik, jak w przypadku uproszczonych obliczeń z sumą: $${ B_x = \frac{\mu_{0}}{2\pi} \frac {I \pi R ^{2}} {r^3} }$$ Na koniec wykorzystajmy ten bardzo praktyczny wzór do wykreślenia pola magnetycznego pętli z prądem w programie Excel.
W tym celu załóżmy, że oś pętli z przewodnikiem stanowi jednocześnie oś x z punktem 0 w środku pętli. Przypuśćmy, że przez drut przepływa prąd o natężeniu I = 2A, a sama pętla ma promień R = 0,25 m. Obieramy 11, symetrycznie rozłożonych punktów na osi (od -0,25, do +0,25 m) i dla nich obliczamy indukcję pola magnetycznego B_x – rysunek 4.
a)
b)
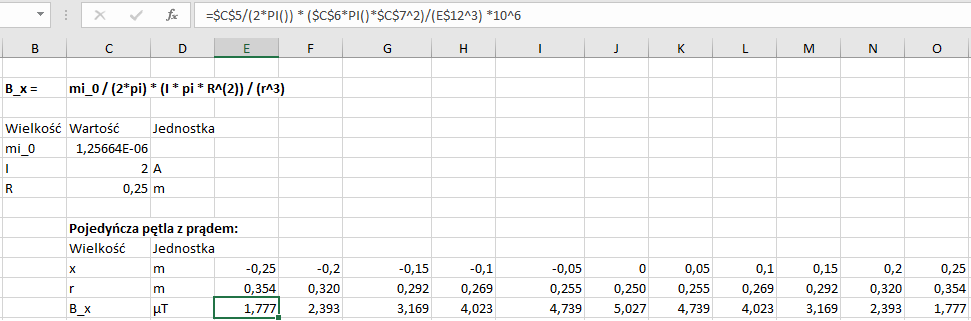
Otrzymane wartości indukcji pola możemy nanieść na wykres, w którym oś pozioma odpowiada osi x z rysunku 4a, a oś pionowa – obliczonym wartościom indukcji – rys. 5
Rys. 5. Pole magnetyczne pętli z prądem otrzymane na podstawie wzoru 2. Pole ma największą wartość w płaszczyźnie pętli.
Solenoid, cewka elektryczna
Jak wspomniano już wcześniej, solenoid można potraktować jako szeregowo połączone pętle z prądem. Co prawda takie zamodelowanie nie umożliwia prostego obliczenia pola magnetycznego cewki „na papierze”, jest jednak świetnym podejściem, gdy chcemy zastosować metodę numeryczną.Kontynuujmy rozważania w programie Excel rozpoczęte w poprzednim paragrafie. W każdym z obranych punktów na osi x ustawmy przewodzącą pętlę o promieniu R = 0,25 m. Łączymy je szeregowo i przepuszczamy prąd o natężeniu I = 2A. W ten sposób otrzymaliśmy prosty model cewki.
Procedurę obliczenia pola, jaką poprzednio zastosowaliśmy do pojedynczej pętli, teraz powtarzamy 11 razy. Wszystkie wyniki do siebie dodajemy. Tutaj, ze względu na dużą liczbę obliczeń, przedstawiona jest jedynie tabela podsumowująca – rys. 6.
Rys. 6. Indukcja pola magnetycznego w prostym modelu cewki. Wyniki są sumą indukcji z 11 pętli z prądem.
Tak jak i poprzednio, wyniki obliczeń przenosimy na wykres – rys. 7.
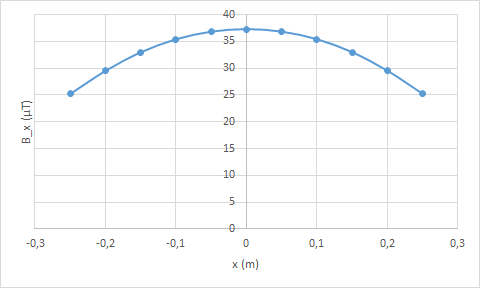Rys. 7. Pole magnetyczne cewki – model złożony z 11 pętli z prądem.
Otrzymany wykres pola cewki jest bardziej płaski, niż wykres dla pojedynczej pętli (rys. 5). Efekt spłaszczenia otrzymaliśmy już przy 11 pętlach. Jaki byłby wykres, gdyby pętli było 100, 1000 lub 10 000? Okazuje się, że gdybyśmy dokładali kolejne pętle do naszego układu, to w pewnym momencie otrzymany wykres byłby już całkowicie płaski. Jest to ważny, praktyczny wniosek:
pole wewnątrz cewki jest jednorodne (stałe).
Cewka elektryczna – prawo Ampere’a
Pole magnetyczne cewki można obliczyć również analitycznie, z zastosowaniem prawa Ampere’a. Prawo Ampere’a mówi, że „cyrkulacja wektora indukcji pola magnetycznego po dowolnej krzywej zamkniętej jest równa iloczynowi natężenia prądu przepływającego przez powierzchnię ograniczoną przez tą krzywą i przenikalności magnetycznej”. Tę długą definicję można również wyrazić wzorem: $${ \oint_l \vec B \vec dl = \mu_0 I \tag{5} }$$
Rys. 8. Prawo Ampere’a dla cewki. Obieramy prostokąt o dwóch bokach równoległych do osi cewki – jeden bok wewnątrz, a drugi na zewnątrz solenoid.
Przy tak obranej krzywej, całkę wyrażającą cyrkulację można łatwo uprościć i zapisać jako sumę czterech wyrazów:
$${ \oint_l \vec B \vec dl = \int_{A}^{C} \vec B \vec dl_{AC} + \int_{C}^{D} \vec B \vec dl_{CD} + \int_{D}^{B} \vec B \vec dl_{DB} + \int_{B}^{A} \vec B \vec dl_{BA} }$$
Przyjmijmy, że nasza cewka ma długość znacznie większą od średnicy. Można wykazać, że taki solenoid ma jednorodne pole wewnątrz oraz zerowe na zewnątrz pierścieni. Założenie to nie jest „wyssane z palucha” – doświadczenia pokazują, że rzeczywiście pole cewki z dużą dokładnością tak się zachowuje.
Nasz wzór na cyrkulację upraszcza się. Zauważmy, że pole B_BA = 0 oraz następnie:
$${ \int_{B}^{A} \vec B \vec dl_{BA} = \int_{B}^{A} \vec B_{BA} \vec dl_{BA} = 0 }$$
$${ \int_{A}^{C} \vec B \vec dl_{AC} = \int_{A}^{C} B_{AC} dl_{AC} cos (90^o) = 0 }$$
$${ \int_{D}^{B} \vec B \vec dl_{DB} = \int_{D}^{B} B_{DB} dl_{DB} cos(90^o) = 0 }$$
Zatem:
$${ \oint_l \vec B \vec dl = \int_{C}^{D} B dl_{CD} cos(0^o) = B_{CD} l_{CD} }$$
Wróćmy do wzoru Ampere’a. Przyjęta ramka obejmuje n pętli z prądem, zatem przez ramkę przepływa prąd o natężeniu nI. Korzystając z tego wniosku oraz wyniku wyznaczonej cyrkulacji otrzymujemy wzór na wartość indukcji wewnątrz cewki:
$${ B_{CD} = \frac{ \mu_0 nI }{ l_{CD}} = \mu_0 NI }$$
Gdzie N – gęstość ułożenia zwojów
Cewka Helmholtza
Jak już wcześniej wspomniano, główną zaletą cewek elektrycznych jest generowanie jednorodnego pola magnetycznego o łatwej do obliczenia wartości. Gdybyśmy jednak chcieli skonstruować taki przyrząd, mogłoby się okazać, że potrzebujemy dużej ilości ciężkiego drutu miedzianego, a sam obszar wewnątrz cewki będzie trudno dostępny dla eksperymentatora. Alternatywą jest zbudowanie cewki Helmholtza. Jest to układ dwóch cewek o takim samym promieniu, ułożonych współosiowo i oddalonych od siebie o odległość równą promieniowi cewek – rysunek 9. W najprostszym przypadku cewki mogą stanowić pojedyncze pętle z prądem.
Rys. 9. Cewki Helmholtza wykorzystywane w Głównym Urzędzie Miar w Warszawie jako wzorce natężenia pola magnetycznego [2]
Jak poprzednio, szacujemy wartości indukcji pola magnetycznego w układzie złożonym z dwóch pętli o promieniu 0,25 m oddalonych od siebie o 0,25 m dla 11 punktów na osi x. Liczymy wartości dla każdej pętli według wzoru 3 i dodajemy. Wynik przedstawia rysunek 11.
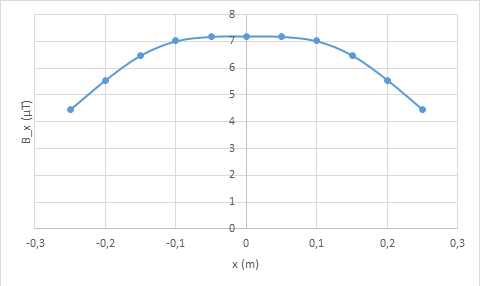
Rys. 10. Indukcja pola magnetycznego cewki Helmholtza złożonej z dwóch pojedynczych pętli z prądem o natężeniu 2A, promieniu 0,25m.
Rys. 11. Miernik pola magnetycznego GM08 [4].
Gradientowa cewka Maxwella
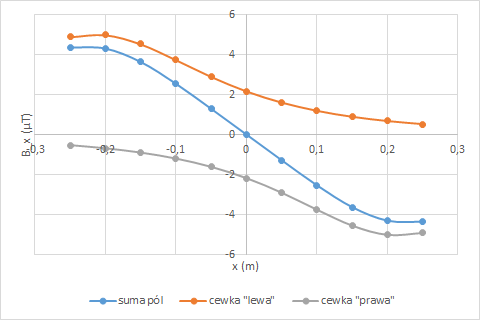Rys. 12. Indukcja pola magnetycznego gradientowej cewki Maxwella złożonej z dwóch pojedynczych pętli z prądem o natężeniu 2A, promieniu 0,25m, odległych od siebie o 0,43m.
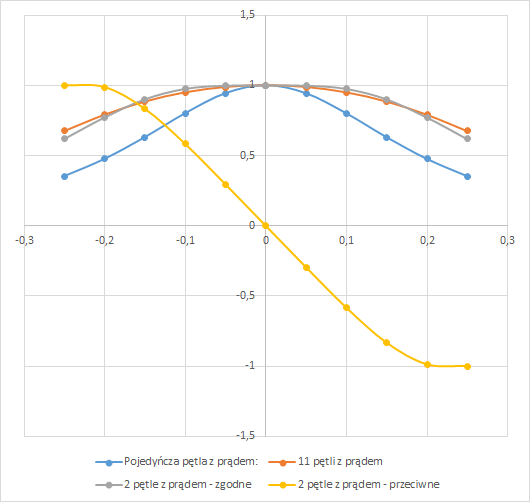
Rys. 13. Porównanie indukcji pola magnetycznego dla różnych typów cewek.
Na koniec tej części tematu warto dodać porównaniu pól omówionych cewek, co pozwoli uwydatnić ich podobieństwa i różnice. Ponieważ interesuje nas kształt krzywych, a nie ich wartości (które łatwo zmodyfikujemy manipulując natężeniem prądu w razie potrzeby), unormujemy wszystkie pola do 1. Jak widzimy na rysunku 13, pole cewki Helmholtza jest niemal identyczne z polem prostego modelu solenoidu.
Tłumienie pola magnetycznego tła, aktywny ekran
Jak wiadomo Ziemia posiada swoje bieguny magnetyczne. Ich istnienie pełni bardzo ważną rolę dla życia na naszej planecie – pole magnetyczne Ziemi „ściąga” pędzące przez przestrzeń kosmiczną naładowane elektrycznie cząstki ograniczając działanie na organizmy promieniowania jonizującego. Drugą stroną medalu jest jednak wpływ pola na urządzenia elektryczne i magnetyczne. Jesteśmy zanurzeni w stałym polu magnetycznym Ziemi o indukcji rzędu kilkudziesięciu nanotesli [5]. O ile urządzenia codziennego użytku nie są czułe na tak małe pola, o tyle precyzyjne pomiary laboratoryjne czy np. pomiary geologiczne mogą wymagać osłonięcia od pola tła. Jak to zrobić?
Rys. 14. Układ trzech cewek Helmholtza o wzajemnie prostopadłych osiach [6]. Taki układ może posłużyć jako ekran dla pola tła.
Szybki teścik
Bibliografia
- Cewka, https://pl.wikipedia.org/wiki/Cewka, dostęp: 23.11.2022
- Cewki Helmholtza - Laboratorium Mikrofal, Pola Elektromagnetycznego i Kompatybilności Elektromagnetycznej, https://www.gum.gov.pl/pl/dziedziny/elektrycznosc-i-magnetyzm/stanowiska-pomiarowe/1389,Laboratorium-Mikrofal-Pola-Elektromagnetycznego-i-Kompatybilnosci-Elektromagnety.html, dostęp: 05.05.2022
- Theoretical And Experimental Analysis Of Magnetic Field Gradients For MRI, https://ieeexplore.ieee.org/document/701859, dostęp: 05.05.2022
- Miernik pola magnetycznego GM08, https://www.merazet.pl/produkt/miernik-pola-magnetycznego-gausomierz-teslomierz-hirst-gm08/, dostęp: 10.05.2022
- Pole magnetyczne Ziemi, https://www.medianauka.pl/pole-magnetyczne-ziemi, dostęp: 10.05.2022
- Jake J. Abbott, Parametric design of tri-axial nested Helmholtz coils, https://aip.scitation.org/doi/abs/10.1063/1.4919400, dostęp: 10.05.2022