26.02.2024r

Prawo rozpadu promieniotwórczego

Spis treści
  1. Jądra stabilne i niestabilne (Ł)
  2. Prawo rozpadu promieniotwórczego (Ś)
  3. Wyprowadzenie wzoru na prawo rozpadu promieniotwórczego i aktywność (T)
  4. Przykład zadania z rozpadem promieniotwórczym - technet Tc-99 (Ś)
  5. Przykład zadania z rozpadem promieniotwórczym - zanieczyszczony technet Tc-99 (T)
  6. Praktyczne wykorzystanie prawa rozpadu promieniotwórczego – datowanie radiowęglowe (Ś)
  7. Rozpad promieniotwórczy w elektrowniach - katastrofa w Czarnobylu (Ś)
  8. Rozpad promieniotwórczy w elektrowniach - katastrofa w Fukushimie (Ś)
  9. Szybki teścik

Prawo rozpadu promieniotwórczego jest przykładem prawa, które opisuje zjawisko całkowicie losowe w sposób ścisły matematycznie. Z taką sytuacją spotykamy się w fizyce wtedy, gdy mamy do czynienia z olbrzymią ilością zdarzeń losowych, a więc przede wszystkim w fizyce jądrowej, kwantowej, czy termodynamice (w podejściu statystycznym). W tym artykule przekonamy się, jak wykorzystywane jest prawo rozpadu promieniotwórczego do datowania radiowęglowego oraz w nauce, np. do opisu skażeń środowiska po katastrofie w Czarnobylu i Fukushimie.

Jądra stabilne i niestabilne

Cała materia zbudowana jest z atomów różnych pierwiastków chemicznych. Obecnie poznano 118 pierwiastków [1], z czego przeszło 90 występuje naturalnie w środowisku, a pozostałe zostały zsyntezowane jedynie z laboratoriach.

Atomy tego samego pierwiastka mogą różnić się od siebie liczbą neutronów zgromadzonych w jądrze. Jądra atomów o różnej liczbie neutronów, lecz tej samej liczbie protonów nazywamy izotopami. Okazuje się, że większość izotopów jakie można otrzymać jest niestabilnych. Oznacza to, że nie jest zachowana równowaga energetyczna w jądrze co prędzej lub później prowadzi do jego rozpadu. Sytuację tę można porównać do napiętej liny, po której chodzi linoskoczek. Doświadczony sportowiec utrzyma się na niej dłużej, amator prawdopodobnie od razu spadnie. Nie da się jednak przewidzieć dokładnie chwili upadku, gdyż ta jest czysto przypadkowa. W takim doświadczeniu stabilne pierwiastki można porównać do rozwieszonych na sznurze, mokrych ubrań. Trzeba je mocno pociągnąć, żeby spadły. Aktualny, interaktywny układ okresowy pierwiastków chemicznych wraz z wyróżnieniem izotopów został udostępniony na stronie organizacji IUPAC [1]. Na stronie znajduje się również wersja pdf do pobrania.
prawo rozpadu promieniotworczego pierwiastki IUPAC
Rys. 1. Układ okresowy pierwiastków udostępniony na stronie organizacji IUPAC[1]. Na stronie dostępne są również inne informacje, m.in. na temat okresów połowicznego zaniku izotopów.

Prawo rozpadu promieniotwórczego

Prawo rozpadu promieniotwórczego jest podstawowym prawem rządzącym światem fizyki jądrowej. Ma ono postać prostego, intuicyjnie zrozumiałego wzoru – określa ono liczbę jąder danego izotopu pozostających w próbce w zależności od upływającego czasu: $${ N(t) = N_{0} \cdot e^{-\lambda t} \tag{1} }$$ gdzie: N(t) – liczba jąder w próbce w danej chwili t
N0 – początkowa liczba jąder w próbce
λ to tak zwana stała rozpadu. Jest ona powiązana z okresem połowicznego zaniku (czas, po którym rozpadowi ulega połowa jąder z danej próbki) zależnością: $${ T_{\frac{1}{2}} = \frac{ln(2)}{\lambda} \tag{2} }$$ Kolejną, powiązaną z prawem rozpadu promieniotwórczego wielkością jest aktywność próbki. Określa ona liczbę rozpadów obserwowanych w jednostce czasu. Dana jest wzorem: $${ A(t) = A_{0} \cdot e^{-\lambda t} \tag{3} }$$ Gdzie A0 to aktywność początkowa. Jednostką aktywności jest bekerel (Bq) – 1 Bq to jeden rozpad na sekundę. Dawniej stosowaną (a obecnie spotykaną) jednostką aktywności był kiur: 1 Ci = 37GBq.

Wyprowadzenie wzoru na prawo rozpadu promieniotwórczego i aktywność

Wyobraźmy sobie, że mamy próbkę z pewną ilością niestabilnego izotopu. Od czego zależeć będzie liczba rozpadów (ΔN), jaką zaobserwujemy? Gdy się nad tym zastanowić, rozwiązanie wydaje się oczywiste – liczba rozpadów promieniotwórczych będzie tym większa, im więcej jąder izotopu zgromadziliśmy (oznaczmy jako N) oraz im dłużej będziemy prowadzić obserwację (Δt): $${ \Delta N = - \lambda N \cdot \Delta t }$$ Niech lambda będzie nieznanym na razie współczynnikiem proporcjonalności, różnym dla różnych izotopów – w końcu każdy izotop będzie rozpadać się w innym tempie.
Przejdźmy do postaci różniczkowej w celu wyprowadzenia wzoru na prawo rozpadu promieniotwórczego: $${ d N = -\lambda N dt }$$ Porządkujemy zmienne: $${ \frac{dN}{N} = - \lambda dt }$$ a następnie całkujemy obustronnie:
$${ ln (N) = -\lambda t + c \ \ \ \ \ \ \ \ (c - stała \ całkowania) }$$
wyznaczamy liczbę jąder N korzystając z definicji logarytmu: $${ N = e^{-\lambda t} \cdot e^{c} }$$
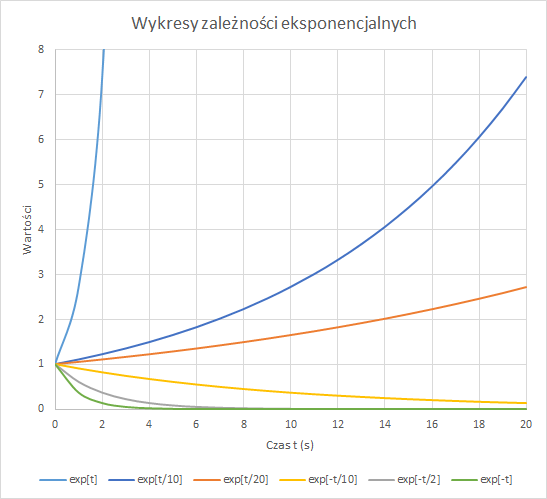prawo rozpadu promieniotworczego wykresy eksponencjalne Rys. 2. Prawo rozpadu promieniotwórczego oraz aktywność próbki można opisać funkcjami eksponencjalnymi o wykładniku ujemnym.
We wzorze pozostała nieznana stała całkowania c – wyznaczamy ją na podstawie warunków początkowych w doświadczeniu. W chwili początkowej t=0 zgromadzona była pewna liczba N0 jąder izotopu: $${ N_{0} = e^{0} \cdot e^{c} = e^{c} }$$ Znając już wartość stałej c, podstawiamy ją do wzoru i otrzymujemy przedstawione wcześniej prawo rozpadu promieniotwórczego: $${ N(t) = N_{0} \cdot e^{-\lambda t} }$$ Wzór na aktywność wyprowadza się ze wzoru na prawo rozpadu promieniotwórczego. Aktywność to liczba rozpadów na jednostkę czasu, a więc: $${ A = -\frac{dN}{dt} = -\frac{d(N_{0} e^{-\lambda t})}{dt} = \lambda N_{0} e^{-\lambda t} = A_{0} e^{-\lambda t} }$$ Jak widzimy, zarówno liczba jąder izotopu pozostająca w próbce, jak i aktywność próbki, to zależności eksponencjalne – rys. 2.

Przykład zadania z rozpadem promieniotwórczym - technet Tc-99

Po zapoznaniu się z prawem rozpadu, przejdźmy do jego praktycznych zastosowań. Na początek zastanówmy się nad prostym przykładem rozpadu izotopu technetu Tc-99. Izotop ten ma okres połowicznego zaniku równy 6h. Jaka część początkowej ilości jąder tego pierwiastka pozostanie po upływie doby?

Do rozwiązania wykorzystać należy wzór 1:
$${ N(24h) = N_{0} \cdot e^{-\frac{ln(2)}{6h} \cdot 24h} = N_{0} \cdot e^{-4ln(2)} = N_{0} \cdot 2^{-4} = 0,0625 N_{0} }$$
Po upływie doby pozostanie 0,0625 (6,25%) początkowej ilości izotopu Tc-99.

Przykład zadania z rozpadem promieniotwórczym - zanieczyszczony technet Tc-99

Zastanówmy się nad następującym problemem, z jakim można spotkać się w laboratorium fizycznym:

Na zajęcia laboratoryjne przywieziono próbkę materiału wykonanego z technetu Tc-99 o okresie połowicznego rozpadu 6h. Podejrzewa się, że w wyniku pomyłki grupy studenckiej próbka technetu mogła zostać zanieczyszczona innym, radioaktywnym izotopem. Wykonano serię pomiarów aktywności próbki – wyniki w tabeli 1.
Tabela 1. Wyniki pomiarów aktywności próbki technetu Tc-99
t (h)
06121824
A (GBq)
31,116,18,74,82,8
Oblicz okres półrozpadu. Czy próbka została zanieczyszczona?

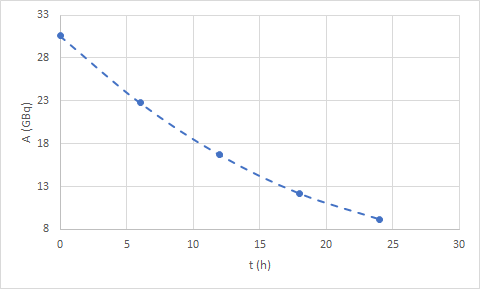prawo rozpadu promieniotworczego aktywnosc technet Rys. 3. Wykres zależności aktywności próbki izotopu technetu Tc-99 od czasu
Na początek zobrazujmy wyniki pomiarów aktywności - nanieśmy punkty pomiarowe na wykres A(t) – rysunek 3.

Na pierwszy rzut oka zależność wygląda poprawnie – aktywność maleje eksponencjalnie. Potrzebne są jednak dokładniejsze wyliczenia. Okres połowicznego rozpadu wyznaczymy dokładnie metodą najmniejszych kwadratów (jeżeli nie znasz tej metody, zapoznaj się z materiałem na stronie pod tym linkiem). Rozważania rozpoczniemy od wzoru 3.: $${ A(t) = A_{0} e^{-\lambda t} }$$ Logarytmując stronami otrzymamy równanie zlinearyzowane na potrzeby MNK: $${ ln(A) = ln(A_{0}) - \lambda t= -\lambda t + ln(A_{0}) }$$
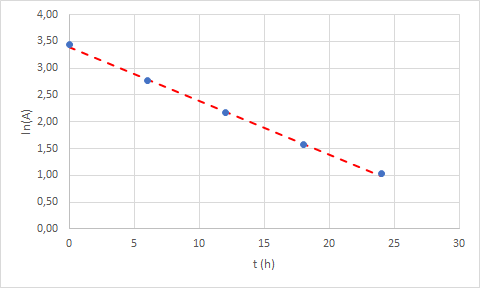prawo rozpadu promieniotworczego aktywnosc technet zlinearyzowany Rys. 4. Prawo rozpadu promieniotwórczego na wykresie - zlinearyzowanazależność aktywności zanieczyszczonej próbki technetu Tc-99 od czasu.
Następnie do zlinearyzowanych punktów pomiarowych na wykresie, możemy dopasować prostą (y=ax+b) – prawdziwe będą wtedy następujące zależności: $${ ln(A_{0}) = b }$$ $${ \lambda = -a }$$ a więc zgodnie ze wzorem 2: $${ T_{\frac{1}{2}} = -\frac{ln(2) }{ a} }$$ Wiemy już, jak obliczyć aktywność zanieczyszczonej próbki i jej okres połowicznego zaniku. Zrealizujmy więc te obliczenia w arkuszu programu excel – program ten ma wbudowaną funkcję do dopasowywania prostej do danych metodą najmniejszych kwadratów. W pierwszym kroku nanosimy punkty na wykres zlinearyzowany ln(N) od t – rysunek 4.

Następnie dopasowujemy prostą metodą najmniejszych kwadratów wykorzystując gotową funkcję excela reglinp – rysunek 5.
prawo rozpadu promieniotworczego aktywnosc technet excel
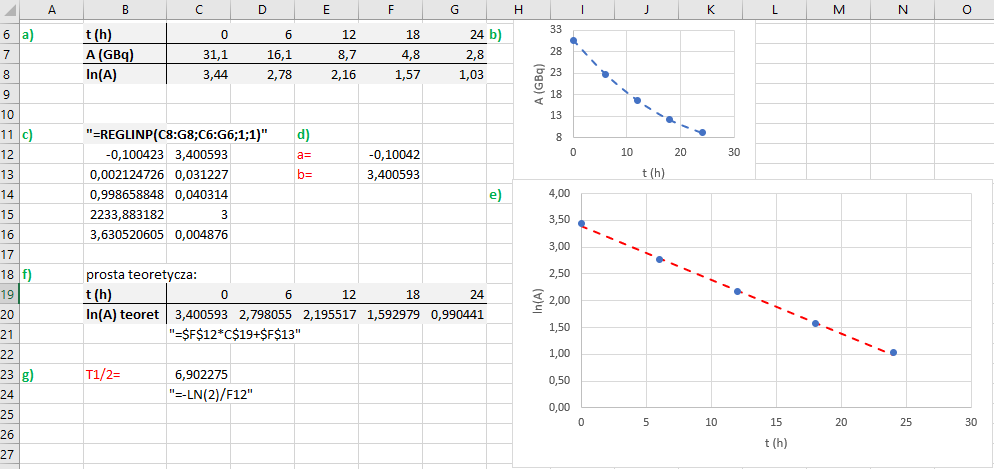
Rys. 5. Wykorzystanie prawa rozpadu promieniotwórczego w laboratorium – metoda najmniejszych kwadratów umożliwia obliczenie okresu połowicznego zaniku izotopu.
Na podstawie wyników funkcji reglinp wyliczamy wartości współczynników funkcji liniowej a i b. Wykorzystując wartość współczynnika a, obliczamy okres połowicznego zaniku badanej próbki: $${ T_{\frac{1}{2}} = -\frac{ln(2) }{ a} = 6,9 h }$$ Otrzymany okres połowicznego zaniku to 6,9 h, a więc możemy stwierdzić, że próbka została zanieczyszczona. Czy da się powiedzieć coś więcej na podstawie tych danych? Jakim izotopem zanieczyszczono próbkę? A może było więcej takich pierwiastków?

Praktyczne wykorzystanie prawa rozpadu promieniotwórczego - datowanie radiowęglowe

Jednym z praktycznych zastosowań prawa rozpadu promieniotwórczego jest datowanie radiowęglowe. Jest to technika umożliwiająca określenie przybliżonego wieku obiektów zbudowanych z węgla (a więc m.in. wszystkich ciał organicznych).

Najpopularniejszym w środowisku naturalnym izotopem węgla jest C-12. Stanowi on 98,89% węgla w środowisku. Poza nim występuje też C-13 (1,11%) oraz radioaktywny C-14 (10^(-10)%) o okresie połowicznego zaniku 5730 lat. Stosunek ilości węgla C-14 do C-12 pozwala określić wiek próbki. W przypadku ciał aktywnie pobierających węgiel ze środowiska, udział izotopów węgla będzie równy temu w środowisku: $${ \frac{^{14}C}{^{12}C} = \frac{10^{-10}\% }{ 98,89\%} = 10^{-12} }$$ Po ustaniu wymiany materii ze środowiskiem (np. po śmierci organizmu żywego), izotop węgla C-14 rozpada się i zanika, natomiast izotop C-12 pozostaje na tym samym poziomie. Oznacza to, że próbka zawierająca np. ¼ ⋅ 10^(-10)% izotopu C-14 (1/4 ilości początkowej) ma około 11 tys. lat (musiały minąć dwa okresy połowicznego rozpadu).

Obecnie stosuje się trzy techniki badania udziału izotopu C-14 w próbkach:
  1. GPC oraz LSC – techniki oparte na zliczaniu liczby emitowanych w rozpadach promieniotwórczych węgla cząstek beta;
  2. AMS – spektroskopia masowa, badanie odchylenia toru cząstki naładowanej w polu magnetycznym, które zależy bezpośrednio od masy cząstki (izotopy węgla C-12 i C-14 różnią się masą).
Jednym z głośniejszych badań wykorzystujących tę własność rozpadu promieniotwórczego był eksperyment z Całunem Turyńskim. Całun został przebadany w 1988 roku przez trzy niezależne laboratoria (Arizona, Zurich i Oxford) metodą AMS. W artykule opublikowanym w Nature[2] czytamy, że płótno całunu z 95% pewnością pochodzi z okresu między 1260 – 1390 r.n.e. Same badania jednak wywołały sporo kontrowersji i zastrzeżeń co do rzetelności ich przeprowadzenia. Właściwe wydaje się więc ponowne przeprowadzenie badania, na to jednak jak dotąd się nie zdecydowano.

Rozpad promieniotwórczy w elektrowniach - katastrofa w Czarnobylu

Katastrofa w Czarnobylu miała miejsce 26 kwietnie 1986 roku, jednak ze względu na decyzje polityczne informacja o wypadku radioaktywnym została upubliczniona na świecie dopiero 28 kwietnia. Wysoki poziom promieniowania został wykryty również na terenie Polski przez specjalnie zbudowane do tego celu detektory promieniowania jonizującego nadzorowane przez Centralne Laboratorium Ochrony Radiologicznej (CLOR). Polskie władze szybko podjęły szereg decyzji mających na celu ograniczenie skutków katastrofy. Jedną z bezprecedensowych decyzji była ta o rozprowadzaniu płynu Lugola wśród dzieci i młodzieży [3].

Tarczyca jest ważnym narządem produkującym hormony - tyroksynę (T4) i trójjodotyroninę (T3). Do produkcji hormonów wykorzystywany jest jod. Niedobór jodu w diecie człowieka może prowadzić do groźnych chorób – o tym, jak ważny jest to pierwiastek dla naszego zdrowia niech świadczy fakt, że sól sprzedawana w sklepach jest nim specjalnie wzbogacana (na opakowaniach spotykamy nazwę „sól jodowana”).

Jednym z najważniejszych izotopów promieniotwórczych uwalnianych w wyniku rozpadu Uranu (w elektrowniach i bombach atomowych), obok cezu-134 i cezu-137 jest jod-131. Ten izotop jodu ma okres połowicznego zaniku ok 8 dni. Rozprowadzanie płynu Lugola (roztworu wodnego bezpiecznego izotopu jodu) po katastrofie miało za zadanie „zapchać” tarczycę, aby ta nie była w stanie wchłaniać izotopu I-131 z nadchodzącej radioaktywnej chmury i skażonego pożywienia. Z tej perspektywy decyzja polskich władz była jak najbardziej trafna, a czas realizacji (roztwór podawano już od 29 kwietnia) wystarczający. Inaczej było w Związku Radzieckim, gdzie środek zaczęto podawać obywatelom po miesiącu od wybuchu reaktora [4]. Po takim czasie podanie płynu nie miało już większego znaczenia dla zdrowia obywateli (zgodnie z prawem rozpadu promieniotwórczego, większość jąder izotopu jodu I-131 już się rozpadło).

Rozpad promieniotwórczy w elektrowniach - katastrofa w Fukushimie

prawo rozpadu promieniotworczego jod 131 japonia Rys. 6. Aktywność izotopu jodu I-131 w próbkach trawy pobranych w czterech miastach w Japonii po wypadku w elektrowni jądrowej[5]. Aktywność izotopu spada eksponencjalnie, co wynika w głównej mierze z rozpadu promieniotwórczego izotopu.
W ostatnich latach również doszło do poważnej katastrofy jądrowej. Miała ona miejsce w Fukushimie w Japonii w marcu 2011 roku. Awaria elektrowni była skutkiem trzęsienia ziemi i powstałej fali tsunami. Podobnie jak w Czarnobylu, doszło do uwolnienia do atmosfery dużej ilości izotopów promieniotwórczych, m.in. cezu-134, cezu-137 i jodu-131. Po wypadku przeprowadzono szereg badań skażenia środowiska. Na rysunku 6. pokazany jest wykres obrazujący skażenie traw izotopem jodu I-131 w różnych japońskich miastach[5].

Na wykresie odłożono aktywność na jednostkę masy próbki (Bq/kg). Aktywność spada bardzo szybko w czasie, co jest związane w głównej mierze z krótkim okresem półrozpadu jodu-131. Warto zwrócić również uwagę, że próbki zbierane w poszczególnych miastach układają się na liniach prostych, co jest związane z linearyzacją danych (logarytm na osi OY) przez autora.

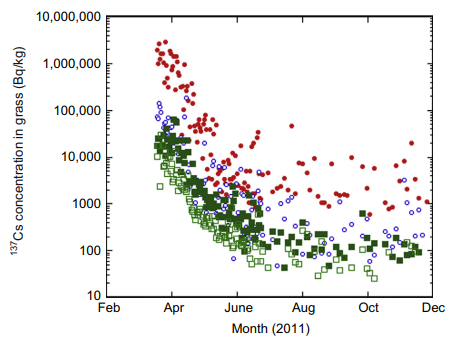prawo rozpadu promieniotworczego cez 137 japonia Rys. 7. Aktywność izotopu cezu Cs-137 w próbkach trawy pobranych w czterech miastach w Japonii po wypadku w elektrowni jądrowej[5]. Aktywność izotopu zanika, co związane jest nie tyle z rozpadem promieniotwórczym, co z wypłukiwaniem pierwiastka przez deszcz i roznoszeniem przez wiatr.
Na rysunku 7. przedstawiono z kolei stężenia izotopu cezu-137 w trawach. W tym przypadku również mamy do czynienia z początkowym szybkim zanikiem izotopu w środowisku. W tym jednak przypadku główną przyczyną nie jest samoistny rozpad (okres półtrwania dla izotopu cezu Cs-137 wynosi aż 30 lat) lecz inne czynniki takie jak opady deszczu i wiatr. Od czerwca 2011 roku obserwuje się stabilizację poziomu izotopu w środowisku.

Jak widzimy, prawo rozpadu promieniotwórczego pozwala wykorzystać zjawisko całkowicie losowe, jakim jest rozpad promieniotwórczy, w bardzo użyteczny sposób – umożliwia zarówno opis i prognozowanie skażeń środowiska, jak i badanie wieku eksponatów historycznych czy próbek geologicznych.

Szybki teścik

Prawo rozpadu promieniotwórczego umożliwia:
W datowaniu radiowęglowym wykorzystuje się zjawisko rozpadu promieniotwórczego izotopu:
Podanie płynu Lugola po miesiącu od katastrofy elektrowni w Czarnobylu nie miało znaczenia dla zdrowia ludności przede wszystkim ze względu na:

Bibliografia

  1. Periodic Table of Elements, https://iupac.org/what-we-do/periodic-table-of-elements/, dostęp: 26.02.2024
  2. P. E. Damon, D. J. Donahue, B. H. Gore i in., Radiocarbon dating of the Shroud of Turin, https://www.nature.com/articles/337611a0, dostęp: 19.01.2022
  3. Kroniki i wspomnienia, Centralne Laboratorium Ochrony Radiologicznej, https://www.clor.waw.pl/images/pliki/historia_clor/CLOR_final.pdf, dostęp: 26.02.2024
  4. Rotkiewicz M., Zabójczy mit Czarnobyla. Ludzi wcale nie trzeba było przesiedlać, https://www.polityka.pl/tygodnikpolityka/klasykipolityki/1514110,1,zabojczy-mit-czarnobyla-ludzi-wcale-nie-trzeba-bylo-przesiedlac.read, dostęp: 19.01.2022
  5. Pavel P. Povinec Katsumi Hirose Michio Aoyama, Fukushima Radioactivity Impact, https://www.sciencedirect.com/science/article/pii/B978012408132100005X, dostęp: 19.01.2022

Komentarze