07.12.2022r

Droga, prędkość, przyspieszenie. Podział ruchów w kinematyce

Spis treści

Tor ruchu. Droga i przemieszczenie (Ł)
Prędkość a szybkość (Ł)
Czy wartość prędkości to szybkość? (Ł)
Przyspieszenie i opóźnienie (Ł)
Podział ruchów. Ruch jednostajny i niejednostajny (Ł)
Rzut ukośny jako suma ruchu jednostajnego i jednostajnie przyspieszonego (Ł)
Szybki teścik

Jednym z podstawowych zagadnień fizyki jest opis ruchów ciał, którym zajmuje się kinematyka. Nauka ta wyróżnia kilka pojęć, takich jak droga, przemieszczenie, prędkość czy tor ruchu i na ich podstawie dzieli sposoby poruszania się ciał na ruch prostoliniowy i krzywoliniowy, jednostajny i niejednostajny. Podział ten jest bardzo praktyczny – sprowadza złożony świat ruchu do kilka prostych wzorów.

Tor ruchu. Droga i przemieszczenie

Mówimy, że ciało porusza się, jeżeli zmienia się jego położenie względem pewnego układu odniesienia. Za układ odniesienia zazwyczaj przyjmujemy ziemię – robimy tak nawet wtedy, gdy nie zdajemy sobie z tego sprawy podając prędkość samochodu (względem ziemi właśnie!) czy położenie obiektu na mapie we współrzędnych geograficznych (ziemskich!). Zauważmy jednak od razu, że ciało będące w ruchu względem ziemi może jednocześnie spoczywać względem innego układu odniesienia – tak jest np. podczas jazdy samochodem. Kierowca przemieszcza się względem jezdni, jednak jest w spoczynku względem fotela w aucie.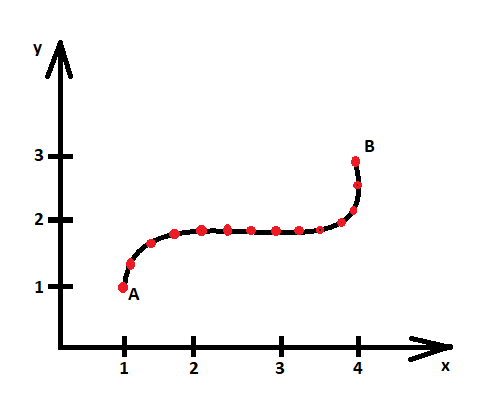

Rys. 1. Tor ruchu punktu materialnego. Tor ruchu zazwyczaj opisujemy w Kartezjańskim układzie współrzędnych (oś x i y, lub x, y i z).

Ciało podczas ruchu zajmuje kolejne położenia (współrzędne) w przestrzeni. Gdy połączymy te położenia linią, otrzymamy tor ruchu. Dobrze jest to zobrazować w układzie współrzędnych – rysunek 1.

Rys. 2. Droga a przemieszczenie. Warto zapamiętać, że droga jest wielkością skalarną (jest długością czarnej linii), natomiast przemieszczenie – wektorową.

Droga (symbol s) w fizyce jest długością toru ruchu, jakim porusza się ciało. Jest to co innego niż przemieszczenie (symbol Δx), które jest różnicą punktu końcowego i początkowego ruchu – rysunek 2.

Zauważmy również, że jeżeli podzielimy nasz ruch na bardzo krótkie odcinki, to poszczególne przemieszczenia będą się pokrywać z torem ruchu. Powiemy wówczas, że suma wartości przemieszczeń jest równa drodze s.

Prędkość a szybkość

Prędkość jest wielkością wektorową, co oznacza że ma wartość oraz kierunek i zwrot – jadący samochód może jechać na przykład z prędkością 50 km/h (wartość), po autostradzie A2 (kierunek wschód – zachód) w stronę Poznania (zwrot).
Prędkość mówi nam, jakie przemieszczenie pokonywane jest w jednostce czasu, co możemy zapisać wzorem: $${ Prędkość: \vec v = \frac{\Delta \vec x} {\Delta t} \tag{1} }$$ Lub w postaci różniczkowej (gdy ruch dzielimy na coraz mniejsze, nieskończenie małe części): $${ Prędkość: \vec v = \frac{d \vec x}{d t} \tag{2} }$$ Wzór 2. nazwiemy jednocześnie definicją prędkości chwilowej. Wartość prędkości pozwala odróżnić ruch jednostajny (prędkość nie zmienia się w czasie) od niejednostajnego (prędkość zmienia się w czasie).

W praktycznych, życiowych sytuacjach często kierunek poruszania się nie jest aż tak istotny. Z takimi problemami mamy do czynienia np. wtedy, gdy pytamy kiedy skończy się paliwo (niezależnie od obranego kierunku ruchu, skończy się tak czy siak), albo jak szybko nasi znajomi jechali nad morze (każdy wie, gdzie jest morze, chodzi nam więc tylko o wartość). W takich sytuacjach będziemy mówić o szybkości. Obliczamy ją dzieląc pokonaną drogę (długość toru ruchu) przez czas ruchu: $${ Szybkość: v = \frac{s}{\Delta t} \tag{3} }$$

Czy wartość prędkości to szybkość?

Powiedzieliśmy już, że prędkość to wielkość wektorowa, posiadająca wartość, kierunek i zwrot. Stwierdziliśmy również, że gdy nie interesuje nas kierunek poruszania się, mówimy o szybkości. Czy można więc powiedzieć, że szybkość to wartość prędkości?

Niestety nie zawsze tak jest – spójrzmy na prosty przykład z rysunku 3.

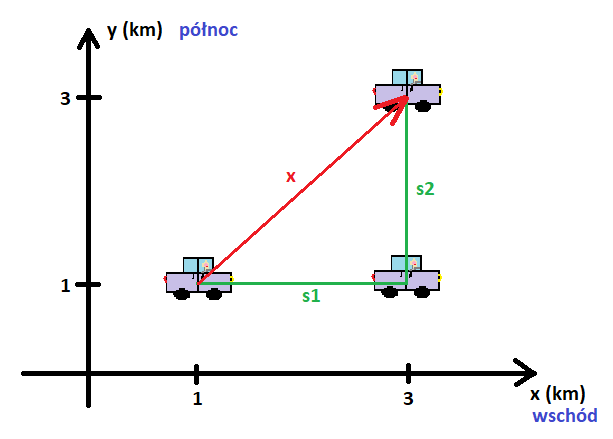
Rys. 3. Droga i przemieszczenie. Jak widać, wartość przemieszczenia nie jest równa drodze, a więc i wartość prędkości nie będzie równa szybkości!

Samochód na rysunku jechał najpierw na wschód, a potem na północ. Całkowita droga wyniosła 4 km. Załóżmy, że czas ruchu to 2 min. Wtedy średnia szybkość poruszania się wyniosła: $${ v = \frac{s}{\Delta t} = \frac{4 ~km} {2 ~min} = 2 \frac{km}{min} }$$ Przemieszczenie jest jednak wektorem (dla „wtajemniczonych”: Δx = (2, 2) km) o zwrocie na północny wschód. Wartość, a więc długość tego wektora policzymy z twierdzenia Pitagorasa: $${ \Delta x = \sqrt{s_{1}^{2} + s_{2}^{2}} = \sqrt{2^{2} + 2^{2}} = 2 \sqrt{2} = 2,82 ~(km) }$$ Średnia prędkość również jest wektorem (v = (1, 1) km/min, czy wiesz dlaczego?) o zwrocie takim samym jak przemieszczenie oraz wartości (zgodnie ze wzorem 2.): $${ v = \frac{\Delta x}{\Delta t} = \frac{2,82 ~km}{2~min} = 1,41 \frac{km}{min} }$$ Jak więc udowodniliśmy, wartość prędkość to nie to samo co szybkość! Możemy jednak wskazać dwie sytuacje, gdy taka równość zachodzi:

ruch jest prostoliniowy, ciało nie zawraca – wtedy długość wektora przemieszczenia będzie równa drodze;
podzielimy ruch na bardzo krótkie odcinki – wtedy poszczególne wektory przemieszczeń pokrywają się z torem ruchu a suma ich wartości będzie równa drodze, o czym mówiliśmy w rozdziale pierwszym.

Żeby jeszcze lepiej zrozumieć różnicę między szybkością i prędkością, a także uzmysłowić sobie jak ważne jest pamiętanie o wektorowym charakterze prędkości, posłużmy się przykładem narciarza zjeżdżającego ze stoku. Zazwyczaj sportowiec nie jedzie po linii prostej, lecz slalomem, więc jego torem ruchu jest zygzak – rysunek 4.

Rys. 4. Tor ruchu narciarza – zygzak.

Narciarz czuje pęd wiatru na swojej twarzy, odczuwa więc, że jedzie bardzo szybko. Droga jaką pokonał, czyli długość toru ruchy, wynosi 900 m. Zjazd trwał półtorej minuty. Średnia szybkość narciarza wyniosła więc: $${ v = \frac{s}{\Delta t} = \frac{900~ m}{90~ s} = 10 \frac{m}{s} }$$

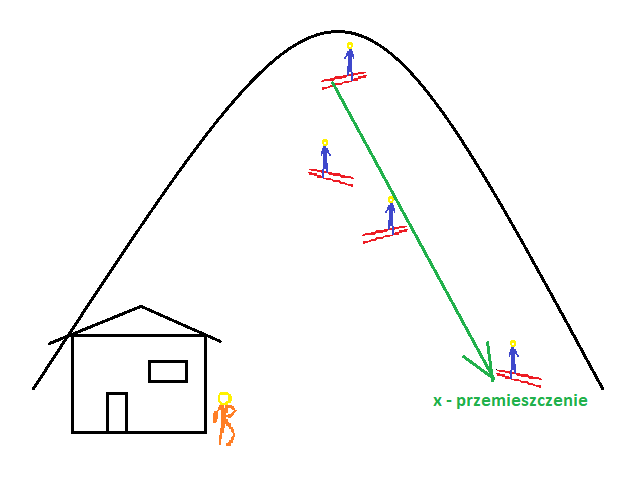Rys. 5. Przemieszczenie narciarza wzdłuż stoku.

Drugi narciarz odpoczywał w stacji narciarskiej u podnóża stoku i od czasu do czasu zerkał na kolegę – rysunek 5. Wydało mu się, że jego przyjaciel przemieszcza się powoli – stok jest niski i jego długość to tylko 300 m! Dla drugiego narciarza obserwowaną i ważną wielkością była średnia prędkość przemieszczania się w kierunku podnóża stoku, która wyniosła: $${ v = \frac{\Delta x}{\Delta t} = \frac{300~ m}{90 ~s} = 3,3 \frac{m}{s} }$$ Gdyby drugi narciarz zerkał na stok częściej to zauważyłby, że kolega jedzie slalomem. Gdyby śledził ruch w sposób ciągły to zaobserwowałby przemieszczenie się wzdłuż rzeczywistego toru ruchu. Stwierdziłby również bez wątpienia, że może i kolega wolno przemieszcza się w dół stoku, ale jednak uzyskuje znaczne prędkości wzdłuż toru ruchu. Gdyby miał do dyspozycji policyjny radar laserowy, to mógłby uzyskać odczyt prędkości równy tej odczuwanej przez zjeżdżającego sportowca.

Przyspieszenie i opóźnienie

Przyspieszenie jest wielkością wektorową, która wyraża jak zmienia się prędkość ciała w czasie: $${ \vec a = \frac{ \Delta \vec v}{\Delta t} \tag{4} }$$ Gdy ciało przemieszcza się coraz wolniej, czyli różnica prędkości jest ujemna, to również przyspieszenie jest ujemne – mówimy wtedy o opóźnieniu. Wartość przyspieszenia pozwala odróżnić ruch jednostajnie przyspieszony i opóźniony (przyspieszenie / opóźnienie stałe w czasie) od ruchu niejednostajnie przyspieszonego i opóźnionego (przyspieszenie / opóźnienie zmienia się w czasie).

Podział ruchów. Ruch jednostajny i niejednostajny

Mamy już zdefiniowane podstawowe pojęcia kinematyki – tor ruchu, droga i przemieszczenie, szybkość i prędkość oraz przyspieszenie i opóźnienia. Teraz możemy przejść do sklasyfikowania ciał ze względu na ich sposób przemieszczania się. Taki podział jest przydatny do sprawnego „przewidywania przyszłości” – przyszłych położeń czy prędkości ciał – poprzez zastosowanie odpowiednich wzorów.

Na rysunku 5 znajduje się schemat z podziałem ruchów w kinematyce. Jest to użyteczna ściągawka – gdy wiemy jakim ruchem przemieszcza się ciało, możemy obliczyć jego przyszłe lub przeszłe położenie i prędkość korzystając z podanych tam wzorów. Wyróżniamy więc ruch jednostajny (gdy prędkość jest stała) i niejednostajny (gdy prędkość się zmienia). Gdy prędkość zmienia się o stałą wartość w każdej sekundzie to mamy ruch jednostajnie zmienny. Gdy zmiana prędkości nie jest stała w czasie, mamy ruch niejednostajnie zmienny.

podzial ruchow jednostajny niejednostajny

Rys. 6. Podział ruchów w kinematyce. Najczęściej rozważa się ruch jednostajny oraz jednostajnie przyspieszony

Podział ten „przemilcza” zagadnienie kierunku ruchu - ruch może być prostoliniowy i krzywoliniowy, zależnie od tego, czy tor ruchu jest linią prostą czy krzywą. Okazuje się również, że ruch krzywoliniowy można w łatwy sposób rozłożyć na sumę ruchów w poszczególnych kierunkach, a do tych z kolei można zastosować wzory ze schematu.

Rzut ukośny jako suma ruchu jednostajnego i jednostajnie przyspieszonego

Przykładem ruchu krzywoliniowego jest rzut ukośny. Wyobraźmy sobie, że rzucamy piłkę „pod skosem do góry” tak, aby piłka pokonała jak największą odległość. Czy taki rzut można opisać według podziału ruchów z rysunku 5?

W tym celu wystarczy, że wyodrębnimy od siebie dwa kierunki przemieszczania się. Jeden poziomy, równoległy do powierzchni ziemi, a drugi pionowy, prostopadły do kierunku ziemi – rysunek 7.

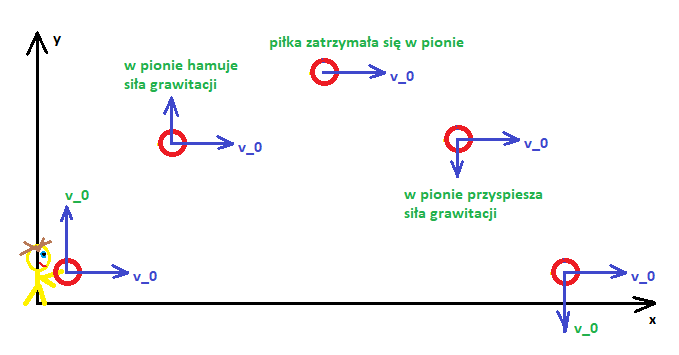
Rys. 7. Rzut ukośny. Ruch piłki można opisać, rozkładając go na przemieszczanie się w dwóch kierunkach – poziomym i prostopadłym do powierzchni ziemi.

Po wypuszczeniu piłki z rąk, przemieszcza się ona ruchem jednostajnym w kierunku poziomym – nadaliśmy jej pewną prędkość początkową, po czym przemieszcza się nie hamowana żadną siłą. Piłka porusza się również ruchem jednostajnie opóźnionym w kierunku pionowym, „do góry” – nadaliśmy jej pewną prędkość początkową, po czym przemieszcza się hamowana przez stałą siłę grawitacji aż do zatrzymania. Następnie zaczyna opadać na ziemię ruchem jednostajnie przyspieszonym – od zatrzymania (prędkość początkowa 0) przyspiesza rozpędzana przez przyciągającą siłę grawitacji aż do zderzenia z ziemią.

Na koniec dodajmy jeszcze, że procedura rozkładania wielkości fizycznych na składowe ma zastosowanie nie tylko w kinematyce, ale jest powszechnie stosowane we wszystkich działach fizyki - świat przyrody i zachodzących w niej procesów jest bardzo złożony, stąd konieczność ciągłego upraszczania modeli fizycznych.