17.05.2022r

Niepewności pomiarowe

Pobierz artykuł w formie Karty Pracy pdf ->

Spis treści

Wartość prawdziwa, błąd przypadkowy i systematyczny (Ś)
Podstawy matematyczne rachunku błędów (Ś)
Wyrażanie niepewności pomiarowych (Ś)
Przykład z multimetrem (Ś)
Poprawny zapis wyników (Ś)
Przykład z pomiarem masy (Ś)
Jeszcze o źródłach niepewności (Ś)
Szybki teścik

Obiektem badań wszystkich nauk przyrodniczych są rzeczywiste obiekty, ciała fizyczne, które możemy poznawać zmysłami. Możemy je widzieć, czuć lub usłyszeć. Podstawowym narzędziem więc dla tych nauk jest pomiar obiektu badania.

Do wykonania pomiaru stosuje się różne przyrządy pomiarowe. Łatwo zauważyć, że przyrządy pomiarowe charakteryzują się różną dokładnością – mamy przecież proste wagi łazienkowe i wysokiej klasy wagi laboratoryjne, centymetry krawieckie i precyzyjne suwmiarki. Wyniki pomiarów są z kolei głównym źródłem wiedzy, podstawą do wyciągania wniosków o otaczającym nas świecie, danym zjawisku czy obiekcie. Stąd tak ważne jest stosowanie precyzyjnych, jednakowych dla wszystkich zasad określania dokładności pomiaru, czy też niepewności wykonanego pomiaru. Międzynarodowa organizacja BIPM opracowała zasady opracowywania danych eksperymentalnych, wydając specjalne zalecenie ISO. Na stronie internetowej organizacji [1] udostępniony do pobrania został przewodnik „Evaluation of measurement data — Guide to the expression of uncertainty in measurement”. Zasad opracowanych przez BIPM przestrzega świat nauki oraz organizacje na całym świecie.

Wartość prawdziwa, błąd przypadkowy i systematyczny

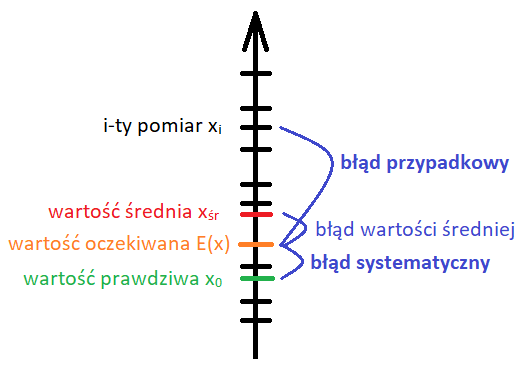Rys. 1. Wartość prawdziwa oraz składowe błędu pomiarowego. Nie możemy zmierzyć wartości prawdziwej, możemy ją jednak oszacować poprzez podanie wartości przybliżonej (np. średniej z kilku pomiarów) oraz wartości błędów.

Na początku warto sobie uświadomić, że każdy pomiar obarczony jest błędem. Nie istnieje doskonale precyzyjny eksperymentator, tak jak nie istnieje idealnie zbudowany przyrząd pomiarowy. Wynika z tego, że wartość prawdziwa charakteryzująca dane ciało nigdy nie zostanie zmierzona, odkryta. Możemy jedynie określić ją „mniej więcej”, podać lepsze lub gorsze jej przybliżenie. Sytuację tę dobrze opisuje wykres na rysunku 1.

Wykonując pomiar popełniamy pewien błąd. Błędem pomiaru nazywamy więc różnicę między wynikiem naszego pomiaru a wartością prawdziwą: $${ \Delta x = x_{0} – x_{i} }$$ Błąd może mieć dwie składowe – błąd przypadkowy i systematyczny. Pierwszy z nich jest związany ze zjawiskiem losowości: na przykład mierząc wzrost osoby przykładamy nieco inaczej miarkę w kolejnych próbach, lub mierzona osoba się wierci. Skutkuje to uzyskiwaniem nieco innych wyników przy każdej z prób. Drugi z nich wynika z metody pomiaru czy jakości przyrządu pomiarowego: w przypadku pomiaru wzrostu nie odczytamy wzrostu dokładniej, niż pozwala na to podziałka miarki.

Błąd przypadkowy łatwo jest ograniczyć – zamiast zmierzyć wzrost raz, możemy pomiar wykonać kilka razy i wyciągnąć z wyników średnią. Okazuje się, że im więcej pomiarów wykonamy, tym wynik będzie bliższy wartości prawdziwej. W metrologii wyróżnia się wartość oczekiwaną z serii pomiarowej:

Wartość oczekiwana E(x) to średnia z nieskończonej liczby pomiarów x_i

E(x) nadal nie będzie jednak równa wartości prawdziwej – nadal pozostanie pewien błąd systematyczny, którego wielkości nie określimy dokładnie.

Podstawy matematyczne rachunku błędów

Do określenia niepewności pomiaru niezbędna jest zrozumienie kilku wielkości:
Średnia arytmetyczna: $${ x_{śr} = \frac{ \sum_{i=1}^{N} x_{i} }{ N } } \tag{1} $$ Odchylenie standardowe: $${ \sigma (x) = \sqrt{ \frac {\sum (x_i – x_{śr})^{2}} {N} } } \tag{2} $$ Odchylenie standardowe średniej: $${ \sigma (x_{śr}) = \sqrt{ \frac{\sum (x_i – x_{śr})^{2}} { N(N-1) } } } \tag{3} $$ Wyobraźmy sobie, że mierzymy wzrost naszego kolegi. Zdajemy już sobie sprawę, że trudno nam jest precyzyjnie rozciągnąć miarkę między jego stopami i głową oraz, że kolega jest wiercipiętą. Decydujemy się więc na wykonanie pomiaru 12 razy. Wyniki zapisujemy w tabeli, wyliczamy z nich średnią i odchylenia standardowe, a następnie nanosimy wszystko na wykres – rysunek 2.

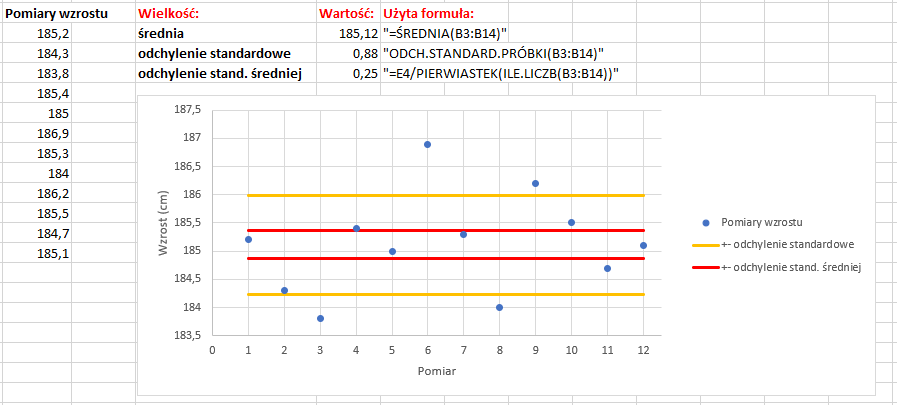Rys. 2. Wyniki pomiarów wzrostu naniesione na wykres. Pomarańczowa i czerwona linia pokazują zakresy wzrostów obejmowane przez odchylenia standardowe.

Jak rozumieć w takim przypadku odchylenie standardowe?

W zakresie wzrostów x_śr +- sigma(x) mieści się 68% wyników pomiarów

W zakresie wzrostów x_śr +- sigma(x_śr) mieści się wartość oczekiwana wzrostu z 68% pewnością

Dodatkowo można stwierdzić, że:

W zakresie wzrostów x_śr +- 2 sigma(x) mieści się 95% wyników pomiarów

W zakresie wzrostów x_śr +- 3 sigma(x) mieści się 99,7% wyników pomiarów

Analogiczne stwierdzenia możemy dopisać dla 2 i 3 sigm dla wartości oczekiwanej

Wartości te są konsekwencją bardzo ważnego stwierdzenia w fizyce – można matematycznie udowodnić, że pomiary w tego typu eksperymentach mają rozkład normalny (Gaussa). Oczywiście zdarzają się eksperymenty, gdzie pomiary mają inne rozkłady, nie mniej rozkład Gaussa jest bardzo powszechny i możemy go na nasze potrzeby przyjmować „w ślepo”.

Wyrażanie niepewności pomiarowych

Najważniejszą wielkością określającą błąd pomiaru jest niepewność standardowa. Jest ona sumą wszystkich rodzajów niepewności, jakie eksperymentator jest w stanie zdiagnozować. Wyraża ona przedział, w jakim zawiera się poszukiwana wartość prawdziwa z 68% pewnością.

Przewodnim ISO podaje dwie metody wyznaczania wartości niepewności standardowej:
Metoda A: w przypadku, gdy mamy serię pomiarów, niepewnością standardową jest odchylenie standardowe średniej z serii (porównaj z przykładem ze wzrostem) $${ u_{A}(x) = \sigma(x_{śr}) } \tag{4} $$ Powszechnie przyjmuje się, że seria pomiarowa powinna mieć co najmniej 12 pomiarów. Liczba pomiarów zależna jest jednak od dokładności, jaką chcemy uzyskać.
Metoda B: zakładamy pewną niepewność graniczną (maksymalną). Niepewność standardowa jest równa niepewności granicznej podzielonej przez sqrt(3) $${ u_B(x) = \frac{\Delta x_{max} } {\sqrt(3) } } \tag{5} $$ Niepewność standardowa jest pierwiastkiem sumy kwadratów wszystkich niepewności:

$${ u(x) = \sqrt { u_{A1}^{2}(x) + u_{A2}^{2}(x) + … + u_{B1}^{2}(x) + u_{B2}^{2}(x) +… } } \tag{6} $$

Wróćmy do przykładu ze wzrostem. Wykonaliśmy serię 12 pomiarów miarką o podziałce równej 1mm. Zauważyliśmy już, że jedną z przyczyn błędów jest przypadkowy rozrzut wyników. Jest to niepewność typu A, którą wyrazimy poprzez odchylenie standardowe średniej. $${ u_{A}(x) = 0,25 cm = 2,5mm } $$ Czy są inne źródła błędów w tym pomiarze? Zwróćmy uwagę, że nasze odczyty mają skończoną precyzję – nie odczytamy wyniku dokładniej, niż pozwala na to podziałka. 1mm jest więc naszą niepewnością graniczną typu B: $${ u_{B}(x) = \frac{1mm}{\sqrt{3}} = 0,67mm } $$ Niepewność standardowa pomiaru wynosi: $${ u(x) = \sqrt{2,5^{2} + 0,67^{2}} = 2,6 (mm) } $$

Przykład z multimetrem

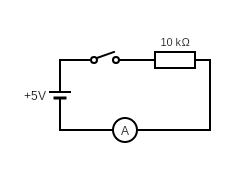Rys. 3. Schemat układu do pomiaru natężenia prądu

Chcemy zmierzyć natężenie prądu płynącego w obwodzie jak na rysunku 3. Włączmy w obwód multimetr przełączony w tryb pomiaru natężenia prądu na zakresie 20 mA i zamykamy obwód włącznikiem. Okazuje się, że multimetr pokazuje stałą wartość 0,48mA. Czy możemy uznać, że wyznaczyliśmy natężenie prądu bez błędu, skoro wartość nie fluktuuje?

Producenci przyrządów pomiarowych najczęściej podają w instrukcji lub na opakowaniach metodykę wyznaczania niepewności pomiarowych. W przypadku prostych multimetrów najczęściej znaleźć można takie lub podobne sformułowanie: $${ \pm \, 0,9\% \, rdg \, \pm 3 \, dgt } $$ Oznacza ono, że niepewność graniczna dla pomiaru wynosi 0,9% odczytu (ang. reading) + 3 cyfry (ang. digits, chodzi o najmniejszą cyfrę, jaką można odczytać z pomiaru). W przypadku naszego pomiaru niepewności prezentują się więc następująco: $${ u_A(x) = 0 } $$

$${ u_B(x) = \frac{0,9\% \cdot 0,48 + 3 \cdot 0,01}{\sqrt{3}} = \frac{0,034}{1,73} = 0,02 (mA) } $$

$${ u(x) = \sqrt{0^{2} + 0,02^{2}} = 0,02 (mA) } $$

Poprawny zapis wyników

Podając wyniki przeprowadzonych pomiarów należy przestrzegać zasad:

Wynikiem pojedynczego pomiaru jest odczyt z przyrządu, wynikiem eksperymentu z serią pomiarów – średnia arytmetyczna
Wynik zawsze podajemy z niepewnością
Niepewność najczęściej podajemy jako niepewność standardową dopisaną w nawiasie, np.: $${ 10,2 (0,1) \, A \,\,\,\,\, lub \,\,\,\,\, 10,2(1) \, A } $$ – oba zapisy oznaczają to samo i są poprawne
Niepewność można podać jako niepewność graniczną – wtedy zapisujemy +-, np.: $${ 10,2 \pm 0,2 \, A } $$
Niepewność podajemy z co najwyżej dwoma cyframi znaczącymi. Najlepiej przyjąć zasadę, że jeśli pierwsza cyfra znacząca to „1” lub „2”, to podajemy dwie cyfry znaczące, natomiast jeśli „3” i więcej – jedną. Niepewności ZAWSZE zaokrąglamy w górę. Przykłady: $${ 0,483 \, A \,\Rightarrow \, 0,5 \, A } $$ $${ 0,2333 \, A \, \Rightarrow \, 0,24 \, A } $$ $${ 5,28 \, A \, \Rightarrow \, 6 \, A } $$
Wynik pomiaru podajemy z liczbą cyfr znaczących odpowiadającą niepewności. Wynik pomiaru zaokrąglamy zgodnie z zasadami matematyki (od „5” w górę, poniżej „5” – w dół), na przykład:
$${ U = 1,275 V \,\,\, i \,\,\, u(U) = 0,12 V \,\,\, \Rightarrow \,\,\, U = 1,28(12) V \,\,\, lub \,\,\, U = 1,28(0,12) V } $$

$${ P = 133,24 W \,\,\, i \,\,\, u(P) = 6W \,\,\, \Rightarrow \,\,\, P = 133(6) W } $$

W przytoczonych wcześniej przykładach wynik pomiaru wzrostu możemy zapisać: $${ Wzrost = 185,1(3) m } $$ Wynik pomiaru natężenia prądu wyniósł: $${ I = 0,48(0,02) mA } $$

Przykład z pomiarem masy

Pan Kowalski postanowił się zważyć na prostej wadze łazienkowej. Po pierwszych próbach zauważył, że wynik na wadze zmienia się, zdecydował się więc na wykonanie serii pomiarowej. Wyniki pomiarów przedstawia tabela 1.

Tabela 1. Wyniki pomiarów masy na wadze łazienkowej

Nr pomiaru	1	2	3	4	5	6	7	8	9	10
Masa	82,9	82,5	81,2	81,5	83,3	78,9	82,6	83,0	81,9	81,0

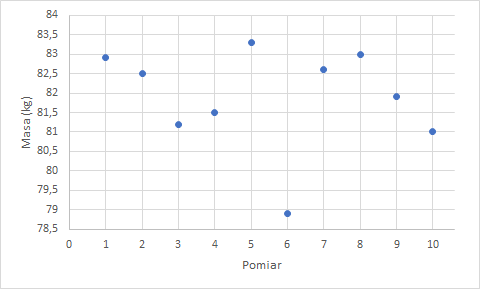Rys. 4. Wyniki pomiarów masy na wadze łazienkowej. Wyniki fluktuują w skończonym zakresie, pomiar 6 wyraźnie odstaje i może zostać odrzucony z badania jako błąd gruby.

Wyniki zostały naniesione na wykres – rysunek 4. Na wykresie łatwo zauważyć, że pomiar 6 wyraźnie odstaje od pozostałych wyników. Taki przypadek należy od razu odrzucić z analizy jako błąd gruby. Dla pozostałych 9 pomiarów obliczamy średnią, odchylenie standardowe i odchylenie standardowe średniej zgodnie ze wzorami 1, 2 i 3. Do tego celu możemy wykorzystać też podane w poprzednim przykładzie formuły programu excel: $${ m_{śr} = 82,21 kg } $$ $${ \sigma(m) = 0,84 kg } $$ $${ \sigma (m_{śr}) = 0,28 kg } $$ Niepewność typu A wynosi więc: $${ u_{A}(m) = 0,28 kg } $$ Teraz niepewność typu B – podziałka wagi to 0,1 kg, a więc niepewność wynosi: $${ u_{B}(m) = \frac{0,1} {\sqrt{3}} = 0,058 kg } $$ Otrzymana niepewność standardowa będzie pierwiastkiem sumy kwadratów niepewności składowych:

$${ u(m) = \sqrt{ u_{A}^2(x) + u_{B}^2(x) }= \sqrt{0,28^2 + 0,058^2} = 0,29 (kg) } $$

Masa pana Kowalskiego wynosi (0,29 kg możemy spokojnie zaokrąglić już w górę): $${ m=82,2(3)kg } $$

Następnego dnia pan Kowalski ponownie stanął na wadze. Okazało się, że przyrząd pokazuje wartości w okolicach 83 kg! Eksperymentator zaczął podejrzewać, że wyniki te są zbyt duże w porównaniu do obliczonej poprzedniego dnia średniej. Jak stwierdzić, czy nie popełniono błędu?

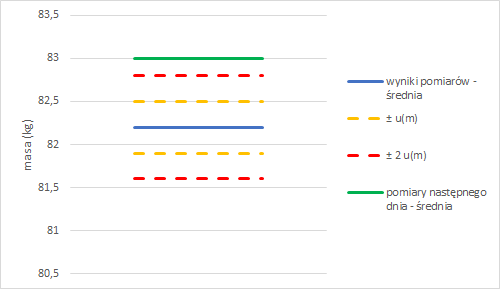Rys. 5. Średnia pomiarów masy wykonanych na drugi dzień znacząco różni się od poprzedniej średniej. Wynik ten nie mieści się ani w przedziale +- u(m) (w którym prawdziwa masa powinna mieścić się z 67% pewnością), ani w przedziale +- 2 u(m) (w którym prawdziwa masa powinna mieścić się z 95% pewnością!)

Na rysunku 5. przedstawiono porównanie wyników średnich z dwóch dni. Jak widać nowa średnia wykracza poza poprzednio obliczoną wagę o więcej, niż niepewność oszacowania. Jesteśmy więc pewni, że popełniono błąd. Co może być jego źródłem?

Pan Kowalski wykonał pomiary w ciągu kilku minut. Nie wziął pod uwagę fizjologii organizmu – być może rano następnego dnia zjadł obfite śniadanie i wypił dużą kawę? Fizjologia organizmu jest kolejnym źródłem niepewności! Pan Kowalski może naprawić swój błąd na dwa sposoby:

Dzienna zmienność masy ciała jest zjawiskiem losowym. Można więc wykonać serię pomiarów nie w ciągu kilku minut, lecz o losowych godzinach w przeciągu kilku kolejnych dni. Otrzymana zmienność będzie znacznie większa i uwzględni dwa zjawiska – fizjologię i losowość przyrządu pomiarowego (Niepewność typu A)
Masa ciała nie zmienia się w nieskończonym zakresie. Zdroworozsądkowo możemy przyjąć, że wartością graniczną jest np. 1 kg i na jej podstawie obliczyć niepewność standardową (Niepewność typu B).

Zastosujmy drugą metodę. Błąd graniczny wynosi 1 kg, a więc niepewność standardowa typu B wynosi: $${ u_{B2} (m) = \frac{1}{\sqrt{3}} = 0,58 kg } $$ Całkowita niepewność standardowa, złożona z trzech składowych wyniesie:

$${ u(x) = \sqrt{ u_{A}^2(x) + u_{B1}^2(x) + u_{B2}^2(x) } = \sqrt{ 0,28^2 + 0,058^2 + 0,58^2}= 0,65 (kg) } $$

Masa pana Kowalskiego z uwzględnieniem poprawki wynosi: $${ m = 82,21(65) kg } $$ Na rysunku 6 przedstawione zostało porównaniu średnich mas z dwóch dni z poprawionymi przedziałami niepewności standardowych.

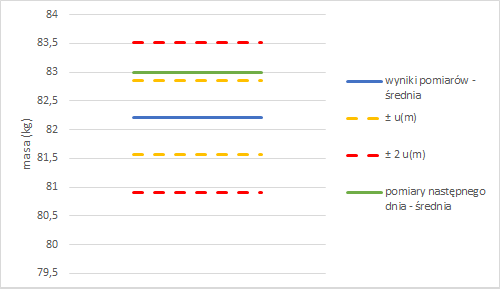Rys. 6. Średnia pomiarów masy wykonanych na drugi dzień nieznacznie wykracza poza obszar +- u(m), a więc nie ma podstaw aby sądzić, że ponownie popełniono błąd w oszacowaniu niepewności

Jeszcze o źródłach niepewności

Zauważmy na koniec, że niepewności z niektórych źródeł są pomijalnie małe w porównaniu do innych. Tak jest w przypadku eksperymentu z masą – niepewność typu B wynikająca z podziałki wagi jest znacznie mniejsza niż dwie pozostałe składowe. Gdybyśmy nie uwzględnili tego składnika, niepewność standardowa pomiaru po zaokrągleniu wyniosłaby dokładnie tyle samo – 0,64 kg (proszę sprawdzić!). Warto mieć to na uwadze – po przeanalizowaniu wszystkich potencjalnych źródeł niepewności eksperymentator może ocenić, które z nich są dominujące i tylko je uwzględnić. Jest to dobry sposób na optymalizację czasu a czasem i kosztów eksperymentu.

Szybki teścik

Bibliografia

Guides in Metrology, https://www.bipm.org/en/publications/guides, dostęp: 26.01.2022
Urbański M. K., Opracowywanie danych doświadczalnych, Wydział Fizyki Politechniki Warszawskiej, 2016