13.05.2024r

Ciało doskonale czarne. Prawo Rayleigha - Jeansa

Spis treści

Czym jest ciało doskonale czarne? (Ł)
Zasada ekwipartycji energii (Ś)
Energia fali elektromagnetycznej w podejściu Rayleigha - Jeansa (Ś)
Prawo Rayleigha - Jeansa dla ciała doskonale czarnego (Ś)
Katastrofa w nadfiolecie (Ś)
Szybki teścik

Zagłębiając się w naukę fizyki można zauważyć, że dyscyplina ta posługuje się w znacznej mierze abstrakcyjnymi obiektami, których nie spotykamy w życiu codziennym. Rozważania nad nimi są jednak praktyczne – przeprowadzając wyliczenia dla prostych modeli, jesteśmy w stanie przewidzieć zachowanie rzeczywistego obiektu. Wśród abstrakcyjnych modeli wyróżnia się ciało doskonale czarne – ta nazwa brzmi niemal magicznie i na pierwszy rzut oka wydaje się być obiektem kompletnie wyssanym z palca. Przy bliższym poznaniu jednak dociera do nas, że taki użyteczny obiekt stanowi dobre przybliżenie właściwie każdego ciała fizycznego, które intensywnie „świeci” cieplnie emitując fale elektromagnetyczne.

W tym artykule skupimy się na analizie rozważań Johna Rayleigha oraz Jamesa Jeansa. Przedstawili oni widmo promieniowania ciała doskonale czarnego, wychodząc jedynie od zasady ekwipartycji energii, która jest jednym z podstawowych praw termodynamiki. Ich wyliczenia doprowadzają do uzyskania sprzeczności, którą nazwano katastrofą w nadfiolecie – niechcący znaleźli oni przypadek, w którym założenia klasycznej fizyki przestają obowiązywać, przyczyniając się do rozwoju fizyki kwantowej.

Czym jest ciało doskonale czarne?

Ciało doskonale czarne to takie, które pochłania całe padające na nie promieniowanie elektromagnetyczne. Oznacza to, że żadna padająca na nie fala nie zostaje odbita. Oczywiście, jest to tylko kolejny abstrakcyjny model fizyczny – w rzeczywistości takie ciała, może poza czarnymi dziurami, nie istnieją. Możemy jednak wskazać kilka obiektów w naszym otoczeniu, które w większym bądź mniejszym przybliżeniu możemy nazwać doskonale czarnymi – obiekty w czarnych kolorach czy wszelkiego rodzaju wnęki z małymi otworami (pokój z oknem, pudło gitary z otworem, ludzkie oko ze źrenicą) rzeczywiście pochłaniają większość padającego na nie promieniowania.

ciemne ubrania cialo doskonale czarne przyklad

Rys. 1. A) Przykład ciała doskonale czarnego w naszym otoczeniu – ciemne ubrania pochłaniają znaczną część promieniowania, przez co nagrzewają się o wiele bardziej niż jasne – odczuwamy to zwłaszcza w słoneczne dni [1]. B) Przykład ciała doskonale czarnego – nie jesteśmy w stanie zobaczyć co znajduje się wewnątrz oka. Promieniowanie elektromagnetyczne wpada przez źrenice i jest całkowicie pochłaniane wewnątrz [1].

Co prawda ciała doskonale czarne pochłaniają całe padające na nie promieniowanie elektromagnetyczne, nie oznacza to jednak, że żadne fale z nich się nie wydostają. Co więcej, z fizycznego punktu widzenia taka sytuacja jest niemożliwa – ciało pochłaniając elektromagnetyczne fale padające nagrzewa się. Nie może jednak nagrzewać się w nieskończoność – musi więc jednocześnie emitować promieniowanie cieplne, dzięki czemu zachowuje stałą temperaturę – jest to stan równowagi termodynamicznej. Łatwo to zrozumieć posługując się przykładem ciemnej koszulki – w słoneczny dzień koszulka taka pochłania wysokoenergetyczne promieniowanie UV oraz widzialne emitowane przez Słońce. Nagrzewa się do często niekomfortowych dla nas temperatur. Nagrzewanie nie trwa jednak w nieskończoność – wraz ze wzrostem temperatury koszulka emituje coraz więcej ciepła (promieniowania podczerwonego, niewidzialnego dla oka). W pewnym momencie temperatura się stabilizuje – energia fal pochłanianych zrównuje się z energią fal emitowanych.

Nieco inaczej wygląda równowaga termodynamiczna gwiazd, żarówek czy świec. W przypadku tych obiektów promieniowanie padające nie ma większego znaczenia – ciała te są same w sobie źródłami nieproporcjonalnie większej energii. Reakcja spalania (w przypadku świecy) czy synteza jąder (w przypadku gwiazd) jest źródłem energii nagrzewającej ciała. Ciała te wraz ze wzrostem temperatury emitują coraz więcej promieniowania cieplnego i, podobnie jak w przypadku czarnej koszulki, dochodzą do stanu równowagi termodynamicznej.

prawo rozpadu promieniotworczego pierwiastki IUPAC

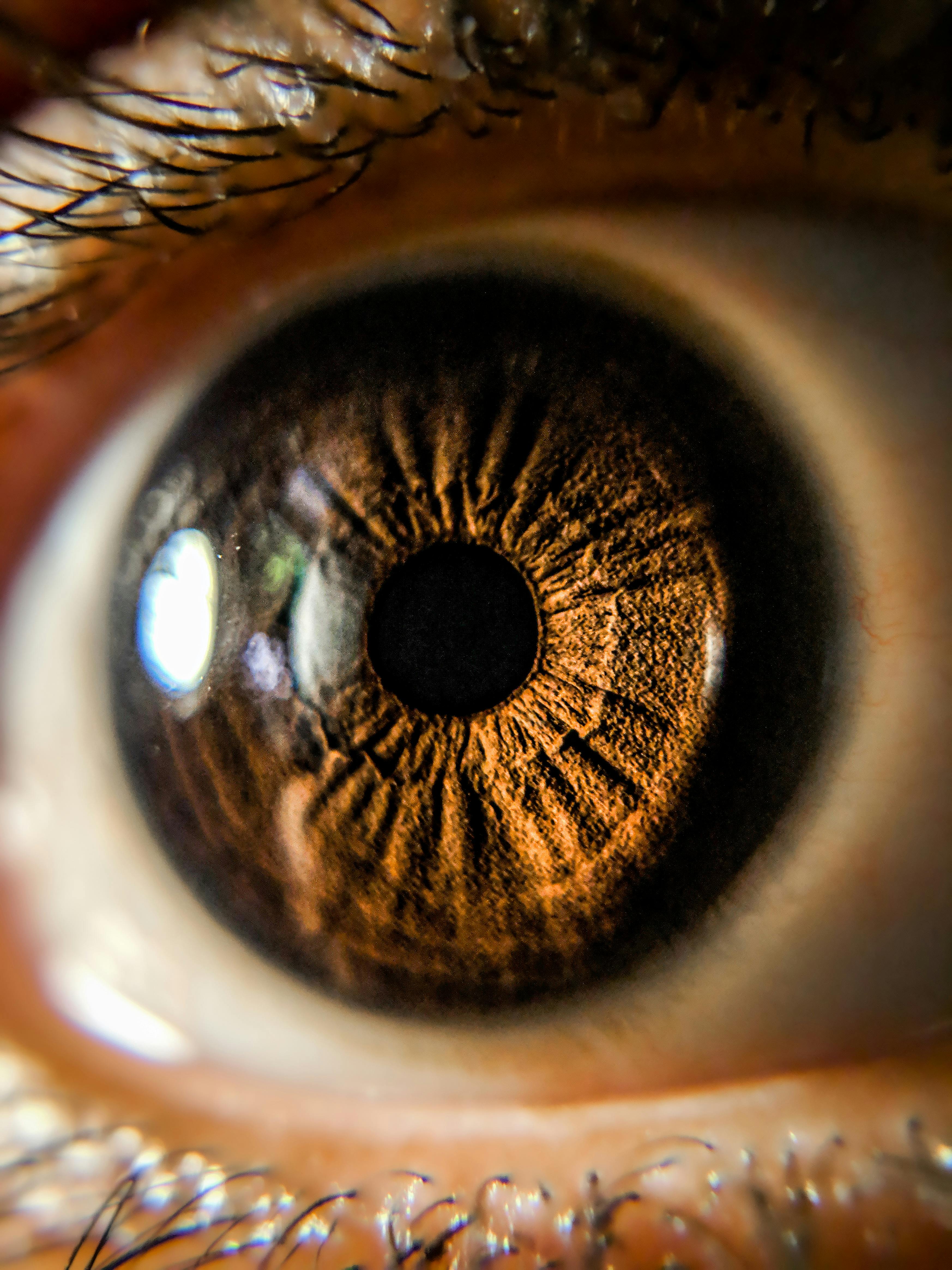
Rys. 2. Słońce jest przykładem ciała doskonale czarnego. W jego przypadku równowaga termodynamiczna jest osiągana przy temperaturze ok 5700 K. W takiej temperaturze emitowane jest głównie promieniowanie z zakresu światła widzianego [1].

Zasada ekwipartycji energii

Zasada ekwipartycji energii jest bardzo prosta, ale jej konsekwencje przekładają się na wiele fizycznych zjawisk. Żeby ją zrozumieć, posłużmy się prostym przykładem – wyobraźmy sobie, że mamy niewielki pojemnik wypełniony swobodnymi cząsteczkami, np. helem. Pojemnik ten utrzymujemy w bardzo niskiej temperaturze, po czym powoli zaczynamy go ogrzewać, a więc dostarczać energię. Które cząsteczki pochłoną tę energię?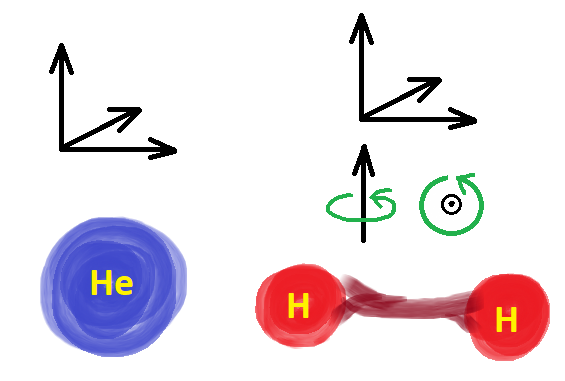

ekwipartycja energii cialo doskonale czarne

Rys. 3. Cząsteczki jednoatomowe posiadają 3 stopnie swobody, a więc ich średnia energia w danej temperaturze wynosi 3/2 k_BT. Cząsteczki dwuatomowe mogą jednak dodatkowo obracać się w dwóch osiach, mają więc aż 5 stopni swobody, a ich średnia energia kinetyczna to 5/2 k_BT. Ile stopni swobody mogą mieć cząsteczki wieloatomowe?

Odpowiedź zdaje się oczywista – wszystkie. Byłoby to niezwykle mało prawdopodobne, aby tylko niektóre cząsteczki kumulowały cała dostarczaną energię, poruszając się coraz szybciej, podczas gdy pozostałe nadal niemal stałyby w miejscu. Zadajmy więc teraz drugie pytanie – w którą stronę poruszałyby się rozpędzane dostarczaną energią cząsteczki? I w tym przypadku odpowiedź narzuca się sama – poruszałyby się chaotycznie, jedne w jedną, drugie w drugą stronę, coraz szybciej tak, że nie dałoby się wyróżnić żadnego z kierunków.

Powyższe proste rozważania zostały ujęte w fizycznej zasadzie ekwipartycji energii – energia dostarczana rozkłada się w postaci energii kinetycznej równomiernie na każdy stopień swobody (każdą cząsteczkę i możliwy kierunek jej poruszania się) w danym eksperymencie. Proste jest też powiązanie średniej energii kinetycznej cząsteczki z temperaturą ciała – można matematycznie wykazać, że każdy stopień swobody kumuluje energię kinetyczną równą ½ k_B T (k_B – stała Boltzmanna). Jeżeli więc mamy cząsteczki helu, które mogą poruszać się w trzech kierunkach, to średnia energia kinetyczna każdej z tych cząsteczek w danej temperaturze wynosi: $${ E_{kin} = \frac{3}{2} k_{B}T \tag{1} }$$

Energia fali elektromagnetycznej w podejściu Rayleigha - Jeansa

Spróbujmy teraz wejść w rolę Reigley’a i Jeansa i prześledźmy ich rozumowanie dotyczące promieniowania ciała doskonale czarnego. Na początek wyrazimy energię pojedynczej fali nawiązując do zasady ekwipartycji energii i pojęcia stopni swobody.

Fala elektromagnetyczna to nic innego, jak przemieszczające się w przestrzeni zaburzenie pola elektrycznego i magnetycznego. Z falą również związana jest pewna energia – wiemy przecież, że źródłem takiej fali może być na przykład drgający ładunek elektryczny. Wytrącony z położenia równowagi ładunek (np. elektron, czy dodatnie jądro w sieci krystalicznej) drga, po czym powraca do stanu równowagi emitując nadmiar energii na zewnątrz właśnie w postaci fali elektromagnetycznej.

Zmodyfikujmy więc nieco nasz eksperyment myślowy dotyczący zasady ekwipartycji energii – dostarczamy energię do ochłodzonych wcześniej cząsteczek tworzących sieć krystaliczną (ciało stałe). Cząsteczki te zaczynają drgać, po czym wyemitowują fale elektromagnetyczne powracając do stanu równowagi. Fale te unoszą pewną energię, zależną od ich stopni swobody. Każdej fali elektromagnetycznej możemy przypisać po dwa stopnie swobody – w tym przypadku są one związane z jej polaryzacją (nie wchodząc w szczegóły, wzajemne przemieszczanie się składowej elektrycznej i magnetycznej fali możemy opisać poprzez dwie wartości). Falom elektromagnetycznym możemy więc przypisać średnią energię związaną z temperaturą danego ciała równą: $${ E = k_{B}T }$$ Powołując się na zasadę ekwipartycji energii dodatkowo musimy stwierdzić, że emisja różnych fal (o różnych długościach) jest tak samo prawdopodobna. Innymi słowy nie jest możliwe, aby ciało emitowało cieplnie fale o określonej długości, pomijając inne długości fal – jest to nielogiczne podobnie jak nielogiczne byłoby rozpędzanie pewnych jąder helu zamkniętych w pudełku, podczas gdy inne nie przyspieszałyby.

Prawo Rayleigha - Jeansa dla ciała doskonale czarnego

fala szescienna wneka cialo doskonale czarne

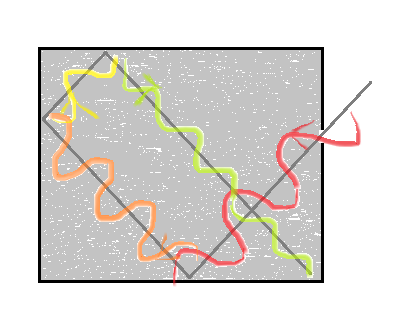Rys. 4. Sześcienna wnęka jako model ciała doskonale czarnego. Fala elektromagnetyczna wpada przez niewielki otwór, po czym odbija się od ścianek wnęki stopniowo wytracając swoją energię.

Wyposażeni w tę wiedzę o emisji cieplnej fal elektromagnetycznych, zastanówmy się jakie widmo powinno emitować ciało doskonale czarne. Naszym modelem ciała doskonale czarnego będzie sześcienna wnęka o niewielkich rozmiarach – rys. 4.

Do sześciennej wnęki przez niewielki otwór wpada promieniowanie elektromagnetyczne – gdy już wpadnie, odbija się od ścianek, a ładunki elektryczne w nich zawarte pochłaniają energię tak, iż fala całkowicie zanika. Aby zachować równowagę termodynamiczną (przy mniejszej czy większej temperaturze), ciało doskonale czarne również musi emitować pewne fale – ładunki elektryczne w ściankach drgają i powracają do stanu równowagi emitując promieniowanie cieplne w postaci fal.

fala emisja szescienna wneka cialo doskonale czarne

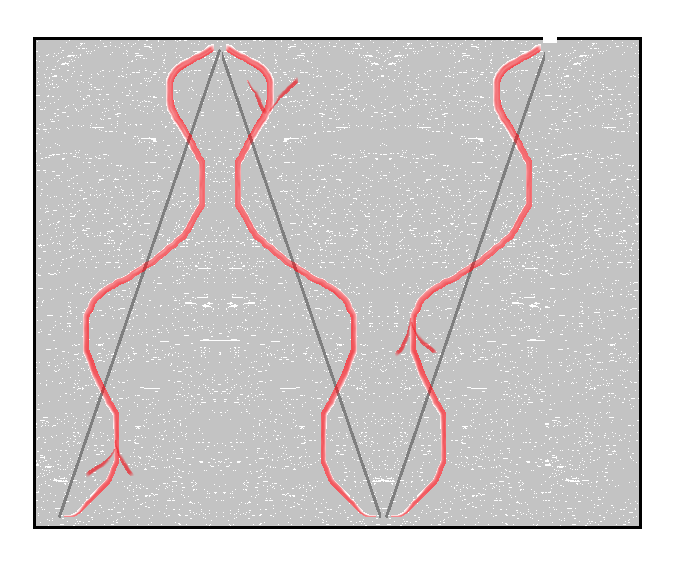Rys. 5. Fala emitowana musi mieć taką długość, aby po dotarciu do ścianki mieć zerową amplitudę – zostanie wtedy całkowicie odbita, gdyż pole elektryczne i magnetyczne na ściankach będzie zerowe, to jest energia fali nie zostanie wykorzystana na pobudzenie ładunków elektrycznych.

Zwróćmy teraz jednak uwagę, że emitowane fale elektromagnetyczne nie mogą mieć dowolnej długości. Aby fala promieniowania cieplnego mogła wydostać się z wnęki, musi się odbijać bez pochłaniania od ścianek naszego sześcianu! W innym przypadku wytraci całkowicie energie, zanim dotrze do otworu – rysunek 5.
Oznacza to ni mniej, ni więcej, że w widmie emitowanego promieniowania cieplnego zobaczylibyśmy tylko fale o pewnych charakterystycznych długościach.

Zastanówmy się teraz nad kluczowym pytaniem – fale o jakich długościach zobaczymy? Więcej będzie fal długich, czy krótkich? A może będzie ich tyle samo?

pilka emisja fali cialo doskonale czarne

Rys. 6. Piłka kopnięta przez piłkarza, aby trafić do bramki, musi znajdować się odpowiednio blisko ziemi. Podobnie fala emitowana przez ciało doskonale czarne, musi mieć zerową amplitudę na szczelinie [1].

Przeprowadzenie dokładnych obliczeń jest dość skomplikowane, skupmy się więc na naszkicowaniu jedynie przybliżonego kształtu widma, jakiego się spodziewamy. Dla uproszczenia więc wyobraźmy sobie, że emitujemy fale z jednego punktu i chcemy trafić szczelinę na przeciwległej ścianie, tak jakbyśmy strzelali piłką do małej bramki – rysunek 6.

emisja fal dlugosci cialo doskonale czarne

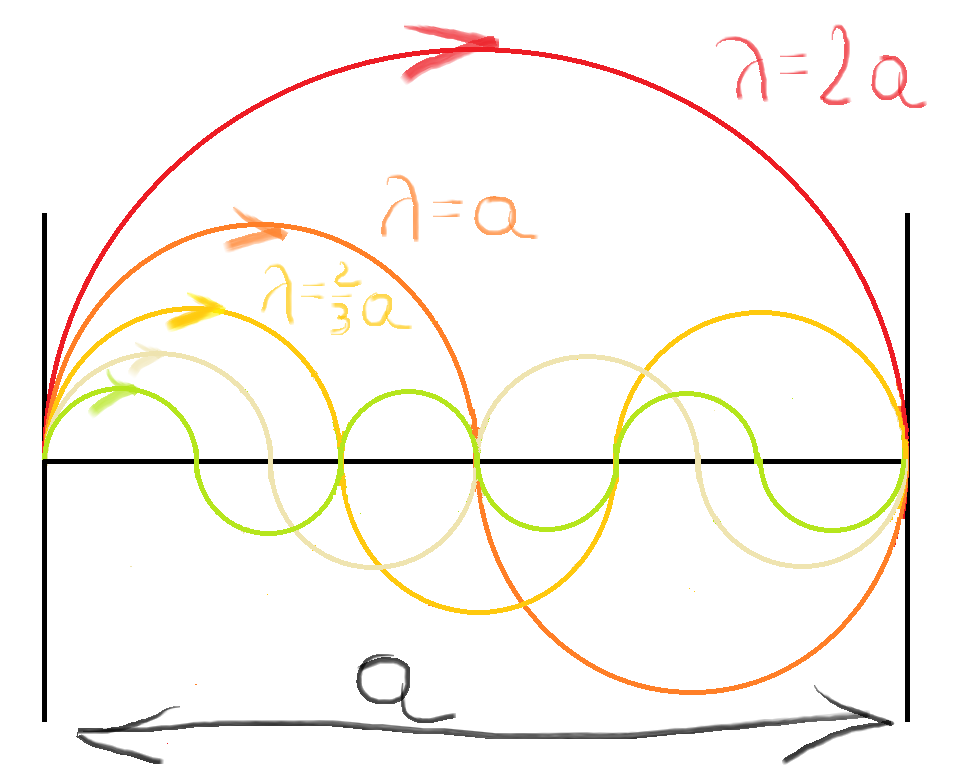Rys. 7. Najdłuższa emitowana fala, jaka może opuścić ciało doskonale czarne, ma długość 2a. Kolejne akceptowalne długości fal to a, 2/3a, 1/2a, 2/5a, 1/3a, 2/7a, 1/8 a, 2/9a, 1/5a, 2/11a, 1/6a, 2/13a, 1/7a…

Jak wcześniej stwierdziliśmy, emisja musi zajść w taki sposób, aby fala miała zerową amplitudę w otworze na przeciwległej ściance. Narysowanie fal o kolejnych dopuszczalnych długościach jest proste... – rysunek 7.

widmo rayleigh jeans cialo doskonale czarne

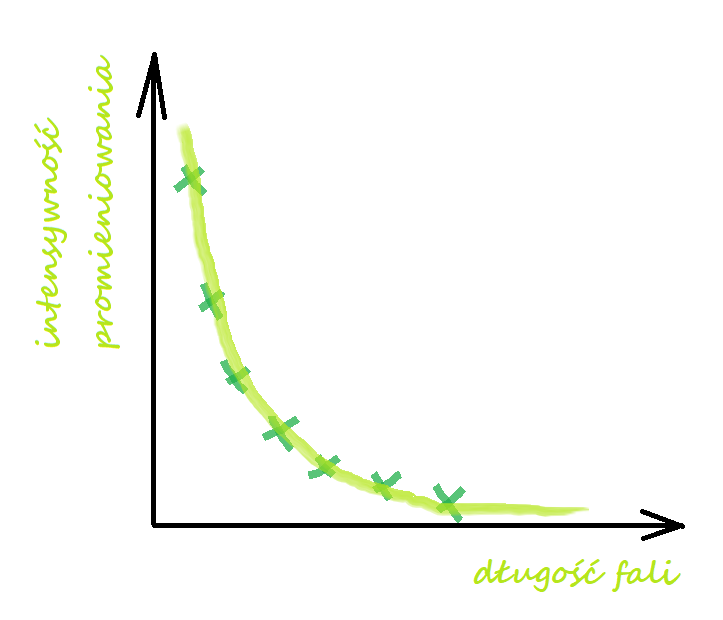Rys. 8. Widmo promieniowania ciała doskonale czarnego w teorii Rayleigha - Jeansa. Intensywność promieniowania (liczba emitowanych fal) dąży do nieskończoności gdy długość fal się zmniejsza oraz do zera gdy rozpatrujemy coraz dłuższe fale.

Jak więc widzimy, jest stosunkowo niewiele możliwych fal o długościach porównywalnych z długością boku a. Możemy jednocześnie wskazać wiele fal krótszych. Przykładowo, możemy narysować tylko jedną falę o długości między 0,45a i 0,55a, 3 fale o długościach między 0,25a i 0,35a oraz aż 5 dopuszczalnych fal o długościach między 0,15a i 0,25a! Gdy przejdziemy do jeszcze mniejszych wartości to zauważymy, że liczba możliwych fal krótkich rośnie eksponencjalnie.

Powołajmy się teraz na zasadę ekwipartycji energii - nie ma powodu, dla którego określone długości fal miałyby być wyróżnione, dlatego wszystkie dopuszczalne w naszym eksperymencie fale są emitowane z takim samym prawdopodobieństwem. W konsekwencji spodziewamy się widma promieniowania o wykresie eksponencjalnym* – rysunek 8.

*Nie określamy w tej chwili dokładnego kształtu widma, a jedynie wyrażamy pewną intuicję. Otrzymalibyśmy nieco inny wykres przy uwzględnieniu wszystkich trzech możliwych kierunków przemieszczania się fali. Dokładne wyprowadzenie można znaleźć w zasobach internetu, np. w [2].

Katastrofa w nadfiolecie

Jak więc wykazaliśmy odtwarzając w uproszczeniu rozumowanie Rayleigha i Jeansa, widmo promieniowania ciała doskonale czarnego powinno być złożone w głównej mierze z fal „krótkich”. Wyniki te wywołały dużo zamieszania w świecie nauki przełomu XIX i XX wieku, ponieważ kompletnie nie zgadzały się z rzeczywistością! Wystarczy przez chwilę zastanowić się nad promieniowaniem wysyłanym przez Słońce – jest ono ciałem w stanie równowagi termodynamicznej, wypromieniowuje więc cieplnie pewną określoną, bardzo dużą, ale jednak skończoną energię. Gdyby więc rejestrować widmo takiego promieniowania, spodziewamy się zobaczyć głównie fale gamma, mniejszą ilość fal ultrafioletowych i sporadycznie fale z zakresu widzialnego i dłuższe. W praktyce jednak obserwujemy bardzo duże natężenie promieniowania już w zakresie widzialnym. Gdyby więc teoria Rayleigha - Jeansa była prawdziwa, intensywność promieniowania nadfioletowego byłaby już tak wielka, że ciało musiałoby emitować niemal nieskończoną energię! Ten paradoks określono historycznie nazwą katastrofy w nadfiolecie. Wielu naukowców głowiło się nad tym problemem poszukując błędu w obliczeniach. Rozwiązaniem okazało się wprowadzenie poprawki już w samych założeniach rozumowania – należało dodatkowo ograniczyć dopuszczalne długości emitowanych fal elektromagnetycznych i powiązać unoszoną przez nie energię z ich długością. Wysiłki te doprowadziły ostatecznie do sformułowania pierwszych praw stanowiących podwaliny mechaniki kwantowej.

Szybki teścik

Teoria Rayleigha - Jeansa:

dobrze charakteryzuje widmo promieniowania emitowanego przez ciało doskonale czarne;

okazała się naukową pomyłką, która przyczyniła się do rozwoju fizyki.

Jeżeli pewne ciało pochłania całe padające na nie promieniowanie, to

nie jesteśmy w stanie go zobaczyć, bo żadna fala elektromagnetyczna się od niego nie odbija;

możemy obserwować jedynie fale z niego emitowane.

Zasada ekwipartycji energii:

pozwala określić średnią energię kinetyczną cząstki na podstawie temperatury ciała;

mówi, że wszystkie cząstki ciała mają taką samą energię kinetyczną;

mówi, że emisja krótszych fal elektromagnetycznych jest bardziej prawdopodobna niż emisja fal dłuzszych.

Bibliografia

Wykorzystano grafiki z serwisu Pexels, https://www.pexels.com, dostęp: 13.05.2024
Deriving the Rayleigh-Jeans Radiation Law, https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/02._Fundamental_Concepts_of_Quantum_Mechanics/Deriving_the_Rayleigh-Jeans_Radiation_Law, dostęp: 13.05.2024