05.11.2022r

Równanie Bernoulliego

Spis treści
  1. Wyprowadzenie równania Bernoulliego (T)
  2. Prawo Bernoulliego - przykłady (Ś)
  3. Paradoks hydrodynamiczny jako konsekwencja prawa Bernoulliego (Ś)
  4. Wykorzystanie różnicy ciśnień do nadawania prędkości statkom (Ś)
  5. Prawo Bernouliego a efekt Magnusa (Ś)
  6. Prawo Bernouliego a rotor Flettnera (Ś)
  7. Szybki teścik

Równanie Bernoulliego jest jednym z najważniejszych praw mechaniki płynów (do płynów zaliczamy ciecze i gazy). Stanowi ono fundament dla dalszych rozważań w termodynamice, pozwala na wyjaśnienie i opis zachowania żagli statków, skrzydeł samolotów, czy rotorów (rodzaj napędu statków). W przeciwieństwie do prawa Ohma, które odkryto dzięki przeprowadzanym doświadczeniom, prawo Bernoulliego wynika z rozważań czysto teoretycznych. Nie oznacza to jednak, że nie ma zastosowania praktycznego, a raczej, że zastosowania znajdowano właśnie dzięki wcześniej dokonanym odkryciom matematycznym.

Wyprowadzenie równania Bernoulliego

bernoulli rura 1 Rys. 1. Przykład prostej instalacji wodnej złożonej z rury z „kolankiem” jako przykład dla zastosowania prawa Bernoulliego
Na początek wyobraźmy sobie instalację wodną wypełnioną cieczą. Dla uproszczenia niech będzie to rura o zmieniającym się przekroju i z „kolankiem”, jak na rysunku 1.

Niepodważalnym prawem fizyki jest zasada zachowania energii. Dla naszego przypadku wygląda ona następująco: $${ E_{pot} + E_{kin} + E_{obj} = const }$$ Lub w postaci różniczkowej: $${ d E_{pot} + d E_{kin} + d E_{obj} = 0 }$$
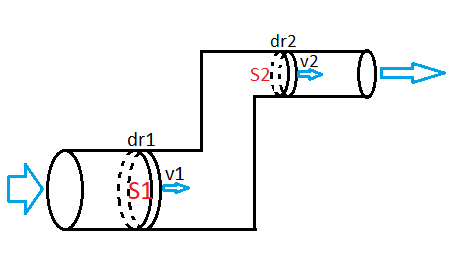bernoulli rura 2 Rys. 2. Zastosowanie prawa Bernoulliego - na rurze wybieramy dwa punkty. Zasada zachowania energii pozwala na wyznaczenie parametrów takich jak ciśnienie i prędkość płynu.
Wybieramy dwa dowolne punkty instalacji – rysunek 2. Do zasady zachowania energii podstawiamy wzory:
$${ mgh_{1} + \frac{mv_{1}^2}{2} + p_{1}V = mgh_{2} + \frac{mv_{2}^2}{2} + p_{2}V }$$
Ostatni z czynników równań, pV, to tak zwana energia objętościowa. Wyraża ona energię niezbędną do „ściśnięcia” płynu. Nie będziemy tutaj wyjaśniać źródeł pochodzenia tego wzoru, jednak intuicyjnie czujemy, że gęściejsze upakowanie cząsteczek wymaga zgromadzenia większej energii. Ponadto jednostką jest dżul ([pV] = Pa * m^3 = N/m^2 * m^3 = N * m = J), a iloczyn kojarzyć należy również z równaniem Clapeyrona (pV = nRT).

Na koniec dzielimy obie strony równania przez masę:
$${ gh_{1} + \frac{v_{1}^2}{2} + \frac{p_{1}}{\rho} = gh_{2} + \frac{v_{2}^2}{2} + \frac{p_{2}}{\rho} \tag{1} }$$
Otrzymany wzór to równanie Bernoulliego. Widzimy na jego podstawie, że znając stan płynu w jednym punkcie, możemy obliczyć jego stan w drugim punkcie. Zanim przejdziemy jednak do praktycznego przykładu, rozważmy jeszcze jedną wielkość – co możemy powiedzieć na pewno na temat prędkości poruszającego się płynu?

Rozważamy płyn nieściśliwy, czyli o stałej gęstości. Załóżmy, że cała instalacja jest już wypełniona płynem. Pompujemy płyn, wywołując jego obieg. W konsekwencji w danym momencie do danej rury wpływa tyle samo płynu, ile z niej wypływa. Stosując język matematyki, możemy ten ważny wniosek zapisać w ten sposób: $${ \frac{dm_{1}}{dt} = \frac{dm_{2}}{dt} }$$ masa to iloczyn gęstości i objętości: $${ \rho \frac{dV_{1}}{dt} = \rho \frac{dV_{2}}{dt} }$$ Jaka będzie ta objętość? W przypadku rury to iloczyn powierzchni S przekroju rury i odległości dr (grubości „plastra” rury, sprawdź na rysunku 2.) $${ \rho S_{1} \frac{dr_{1}}{dt} = \rho S_{2} \frac{dr_{2}}{dt} }$$ zmiana odległości dr w czasie dt ma wymiar prędkości – prędkości przepływu płynu: $${ \rho S_{1} v_{1} = \rho S_{2} v_{2} }$$ $${ S_{1} v_{1} = S_{2} v_{2} \tag{2} }$$ Iloczyn prędkości i powierzchni nazywamy strumieniem prędkości (lub strumieniem objętości). Jest to wzór analogiczny do strumienia pola magnetycznego i elektrycznego.
W powyższym wyprowadzeniu skorzystaliśmy z założenia o stałej gęstości cieczy. Dlatego napiszemy:

Dla cieczy nieściśliwej strumień prędkości jest stały

Prawo Bernoulliego - przykłady

  1. Wyobraźmy sobie instalację wodną w piętrowym budynku. Zazwyczaj woda doprowadzana jest pod powierzchnią ziemi, a następnie rozprowadzana rurami na kolejne piętra. Z równania Bernoulliego (wzór 1.) widzimy, że energia potencjalna wody będzie tym większa, im wyżej będzie się znajdować (czynnik mg). Oznacza to, że musi spadać prędkość przepływu lub ciśnienie (czynnik 2. lub 3.).

  2. Możemy przyjąć, że instalacja domowa jest szczelnie wypełniona wodą. W razie ubytków woda jest uzupełniania w obwodzie poprzez otwarcie specjalnego zaworu. Dodatkowo wiemy, że ściśliwość wody jest bardzo mała. Możemy więc powołać się na prawo stałości strumienia prędkości (wzór 2.) – jeżeli wszystkie rury w budynku mają taką samą średnicę, to prędkość przepływu będzie taka sama, a na wyższych piętrach obniża się ciśnienie wody.

  3. Czasem w wysokich budynkach hydraulicy montują pompy wodne. Zamieniają one energię elektryczną na dodatkową siłę parcia cieczy. Ich zadaniem jest więc zwiększenie ciśnienia w instalacji, pośrednio (zgodnie z prawem Bernoulliego w postaci równania 1.) również na wyższych piętrach.

Paradoks hydrodynamiczny jako konsekwencja prawa Bernoulliego

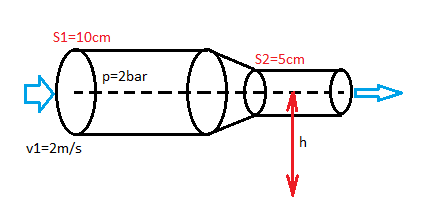bernoulli rura 3 Rys. 3. Intuicja podpowiada, że w węższej części rury przepływająca ciecz będzie miała większe ciśnienie niż w szerszej części. Czy prawo Bernoulliego to potwierdza?
Rozważmy instalację jak na rysunku 3. Rura o zmieniającej się grubości (średnica s1 = 10cm, s2 = 5cm) leży na stałej wysokości nad ziemią. Równanie Bernoulliego (Wzór 1.) upraszcza się więc:
$${ \frac{v_{1}^2}{2} + \frac{p_{1}}{\rho} = \frac{v_{2}^2}{2} + \frac{p_{2}}{\rho} \tag{3}}$$
Jakie jest ciśnienie cieczy w węższej części rury, jeśli w szerszej wynosi 2 bary?
Woda wpompowywana jest do szerszej części rury z prędkością 2 m/s, gęstość wody to 1000 kg/m^3

Znamy parametry początkowe cieczy, czyli jej prędkość i ciśnienie. Prędkość w węższej części rury obliczymy stosując wzór 2.:
$${ v_{2} = v_{1} \frac{S_{1}}{S_{2}} = 2 \frac{\pi \cdot 5^2} {\pi \cdot 2,5^2} = 2 \frac{\pi \cdot 25}{\pi \cdot 6,25} = 8 (\frac{m}{s}) }$$
Teraz pozostaje obliczyć ciśnienie w węższej części rury korzystając ze wzoru 3.:
$${ p_{2} = (\frac{v_{1}^2}{2} - \frac{v_{2}^2}{2} + \frac{p_{1}}{\rho}) \cdot \rho = (\frac{2^2}{2} – \frac{8^2}{2} + \frac{200~000}{1~000} ) \cdot 1~000 = (2 – 32 + 200) \cdot 1~000 = 170~000 (Pa) = 1,7~bar }$$
Jak wykazaliśmy opierając się na równaniu Bernoulliego, ciśnienie w węższej części rury jest mniejsze niż w szerszej części. Zjawisko to wydaje się niezgodne z intuicją, dlatego nazywa się je paradoksem hydrodynamicznym.

Wykorzystanie różnicy ciśnień do nadawania prędkości statkom

Choć nie zdawano sobie z tego sprawy, prawo Bernoulliego było wykorzystywane od wieków. Robili to marynarze na okrętach żaglowych. Do dzisiaj zresztą żeglowanie jest popularnych sportem i wakacyjną rozrywką. O ile fizyka pływania z wiatrem nie jest dla nikogo zagadką, o tyle okazuje się, że można również przemieszczać się… pod wiatr.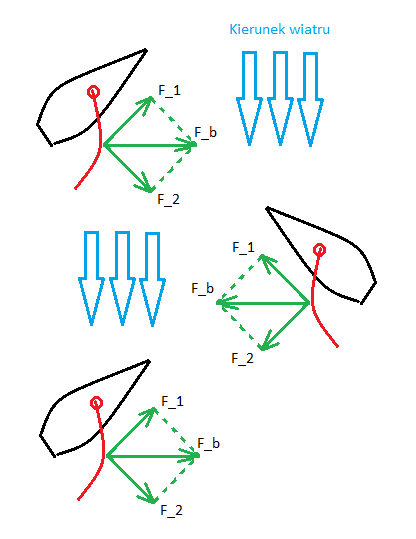

bernoulli zagiel hals
Rys. 4. Halsowanie jako praktyczne wykorzystanie prawa Bernoulliego. Wiatr wypełnia żagiel uwypuklając go. Droga obiegu żagla przez cząsteczki wiatru jest dłuższa ze strony, w którą żagiel jest wypchnięty. Powoduje to powstanie siły o kierunku prostopadłym do żagla.
Pływanie pod wiatr nie odbywa się zgodnie z kierunkiem ruchu wiatru, lecz pod pewnym kątem. W praktyce konieczne jest regularne zmienianie kierunku ruchu na wzór zygzaka – żeglarze często wykonują tak zwane zwroty, a ten styl pływania nazywa się halsowaniem – rysunek 4.

Droga obiegu żagla przez strumień powietrza jest dłuższa od strony, w którą żagiel jest wypchnięty. Jak wiemy z wcześniejszych rozważań na temat prawa Bernoulliego oznacza to, że cząsteczki powietrza będą się z tej strony przemieszczać szybciej, a to przekłada się na niższe ciśnienie. W ten sposób powstaje siła parcia o kierunku (mniej więcej) prostopadłym do płaszczyzny żagla.

Siłę tę warto rozważać poprzez rozłożenie jej na dwa kierunki – zgodny oraz prostopadły do osi łódki. Siła działająca w kierunku osi łódki napędza żaglowiec. Siła prostopadła powoduje dryf statku, jest on jednak znacznie mniejszy, ponieważ opór statku w tym kierunku jest bardzo duży. Siła ta powoduje w głównej mierze pochylenie żaglowca, co jest bardzo widowiskowym zjawiskiem podczas regat – rysunek 5.
bernoulli przechył
Rys. 5. Jachty płynące w silnym przechyle. Za efekt ten odpowiada siła wynikająca z prawa Bernoulliego [1].

Prawo Bernouliego a efekt Magnusa

Prawo Bernoulliego przekłada się również na efekt Magnusa. Jest to zjawisko powstawania siły działającej na obracające się ciało, prostopadle do kierunku ruchu. Możemy je zaobserwować np. podczas lotu „podkręconej” piłki podczas meczu piłkarskiego. W sieci jest też dostępnych dużo efektownych nagrań tego zjawiska fizycznego. Jak taka siła powstaje?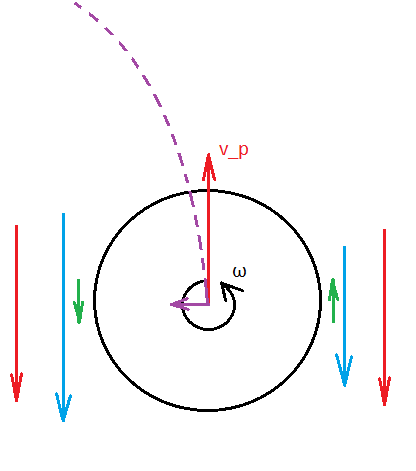

magnus piłka prawo bernoulliego
Rys. 6. Efekt Magnusa i piłka. Kierunek lotu piłki jest wynikiem złożenia kierunku siły, z jaką piłka została kopnięta oraz kierunku siły wynikającej z prawa Bernoulliego, zależnego od ruchu obrotowego.

Kopnięta przez piłkarza piłka porusza się ruchem postępowym z pewną prędkością v_p. Poprzez względność ruchu możemy również powiedzieć, że to powietrze porusza się z prędkością v_p względem piłki. Jeżeli jednak piłkarz dodatkowo „podkręci” piłkę, to nabiera ona również ruchu obrotowego o prędkości kątowej ω. Cząsteczkom powietrza można przypisać pewną lepkość względem poruszającego się ciała – wirujący obiekt nadaje więc dodatkową prędkość cząsteczkom w swoim najbliższym otoczeniu o kierunku zgodnym z ruchem obrotowym – rysunek 6.

Całkowita prędkość cząsteczek powietrza z prawej i lewej strony piłki jest różna. Zgodnie z prawem Bernoulliego (wzór 1.), tam, gdzie jest większa prędkość, występuje niższe ciśnienie. Różnica ciśnień generuje z kolei powstanie siły parcia: $${ F_{p} = p \cdot S }$$

Prawo Bernouliego a rotor Flettnera

Efekt Magnusa, a więc i prawo Bernoulliego, został wykorzystany do budowy rotorów Flettnera. Są to duże, wirujące walce, które obracając się w otoczeniu powietrza o niezerowej prędkości, powodują powstaje siły parcia prostopadłej do tej prędkości. Rotory Flettnera jak na razie nie zdobyły dużej popularności, były jednak wykorzystywane jako napęd na statkach (rysunek 7a i 7b), próbowano wykorzystać je jako napęd samolotów [4], czy turbin w elektrowniach wiatrowych (rys. 7c). W ostatnim czasie coraz głośniej mówi się o wykorzystaniu rotorów jako dodatkowy, wspomagający napęd na wielkich okrętach transportowych. Wykorzystanie tego ekologicznego źródła napędu zyskuje na popularności głownie ze względu na wysokie ceny paliw [6].
a)
rotor flettnera prawo bernoulliego
b)
statek flettner prawo bernoulliego
c)
acowind a 63 flettner prawo bernoulliego
Rys. 7. a) Rotor Flettnera – zasada działania napędu jest oparta na prawie Bernoulliego [2], b) Statek E-Ship 1 wykorzystuje rotory Flettnera jako dodatkowy napęd [3], c) Turbina Acowind A-63 wykorzystująca rotory Flettnera [5]

Szybki teścik

Rozważamy nieściśliwą ciecz przemieszczającą się rurą o zmieniającej się grubości. Zgodnie z równaniem Bernoulliego ciśnienie będzie największe:
Czy aby „podkręcić” kopniętą piłkę musi wiać wiatr?
Rotor Flettnera nadaje prędkość statku o kierunku:

Bibliografia

  1. Przechył, https://www.muratorplus.pl/biznes/wiesci-z-rynku/zeglarski-tydzien-w-dalmacji-viii-regaty-firm-budowlanych-regatta-build-cup-chorwacja-2015-aa-X1ZG-nbuW-hRy3.html, dostęp: 04.03.2022
  2. Rotor jako napęd jednostki pływającej, https://pl.wikipedia.org/wiki/Rotor_Flettnera, dostęp: 04.03.2022
  3. Obracające się cylindry. Alternatywny napęd: żegluga z użyciem rotora Flettnera - nadzieja na efekt, https://technologie.e-magnes.pl/artykuly/nowoczesne-technologie-w-nauce-i-technice/obracajace-sie-cylindry-alternatywny-naped, dostęp: 04.03.2022
  4. Samolot z rotorami Flettnera, https://pl.wikipedia.org/wiki/Samolot_z_rotorami_Flettnera, dostęp: 04.03.2022
  5. Turbina Magnusa, https://zasoby1.open.agh.edu.pl/dydaktyka/inzynieria_srodowiska/c_odnaw_zrodla_en/files/inne_rozwiazania.htm, dostęp: 04.03.2022
  6. Rotory Flettnera dostarczają ogromne oszczędności paliwa, https://www.gospodarkamorska.pl/stocznie-offshore-rotory-flettnera-dostarczaja-ogromne-oszczednosci-paliwa-45268, dostęp: 04.03.2022

Komentarze


Autor: bardzo fajne
Data: 2022-11-17 20:53:32pm
bardzo fajne