17.03.2022r

Opór zastępczy

Spis treści

Opór zastępczy w układzie szeregowym (Ł)
Opór zastępczy w układzie równoległym (Ł)
Obliczanie oporu zastępczego - przykład (Ś)
Przykład oporu zastępczego: transfiguracja trójkąt - gwiazda (T)
Przykład oporu zastępczego: transfiguracja gwiazda - trójkąt (T)
Układ zastępczy opornika, cewki, kondensatora (T)
Szybki teścik

Rzeczywiste układy elektroniczne złożone są z wielu elementów elektronicznych połączonych przewodami (lub np. w przypadku płytek drukowanych ścieżkami przewodzącymi). Wśród tych elementów znajdują się również oporniki. Rezystancję posiadają jednak nie tylko oporniki. Oporność mają również same przewody (ścieżki połączeń), cewki (solenoidy), kondensatory i inne elementy elektroniczne, choć o wartości często na tyle małej w porównaniu do rzeczywistych oporników, że można ją pominąć.

Obliczenie oporu zastępczego umożliwia uproszczenie schematu złożonego układu. Układ zastępczy to taki, w którym napięcia i natężenia prądów nie zmieniły się pomimo zastąpienia kilku oporników jednym. Może więc rodzić się pytanie, po co w ogóle rozważać układy „skomplikowane”, skoro co do wartości napięć i natężeń prądów są równoważne układom „prostym”? Oto przykłady zastosowań:

uzyskanie konkretnej, interesującej nas rezystancji poprzez połączenie kilku oporników jakie posiadamy w warsztacie;
uzyskanie interesujących nas wartości innych parametrów układu, np. napięcia elektrycznego - wymaga to połączenia wielu oporników, choć pod względem oporu można by ten układ zastąpić prostszym;
elementy elektroniczne inne niż oporniki w naszym układzie, np. przewody lub cewki, również mają swoją oporność. Dla uproszczenia obliczeń możemy jednak stworzyć prostszy, matematyczny model - zatąpić kilka wartości rezystancji jedną wartością.

Opór zastępczy w układzie szeregowym

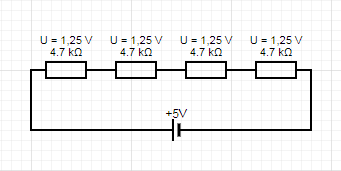Rys. 1. Opór zastępczy - szeregowe połączenie oporników. Napięcie na opornikach sumuje się do napięcia źródła

Szeregowo połączone oporniki przedstawiono na rysunku 1. Połączenie szeregowe występuje np. w lampkach choinkowych lub w dzielniku napięcia. W takim układzie suma napięć na poszczególnych elementach jest równa napięciu źródła. Opór zastępczy dla układu szeregowego oporników obliczamy ze wzoru: $${ R = R_1+R_2+R_3+R_4+… } \tag{1}$$

Opór zastępczy w układzie równoległym

Rys. 2. Opór zastępczy - równoległe połączenie oporników. Napięcie na każdym oporniku jest takie samo, jak napięcie źródła

Równolegle połączone oporniki przedstawiono na rysunku 2. Połączenie równoległe występuje np. w domowej instalacji elektrycznej. W takim układzie napięcie na każdym elemencie jest równe napięciu źródła (w przypadku instalacji domowej, na każdym urządzeniu jest napięcie 230 V). Opór zastępczy dla układu równoległego oporników obliczamy ze wzoru: $${ \frac {1}{R} = \frac {1}{R_1}+\frac {1}{R_2}+\frac {1}{R_3}+ … } \tag{2}$$

Obliczanie oporu zastępczego - przykład

uklad szeregowy rownolegly opor zastepczy

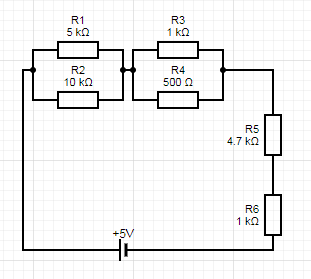Rys. 3. Opór zastępczy możemy policzyć również w bardziej złożonych układach połączeń - tutaj przykładowy układ z opornikami połączonymi szeregowo i równolegle

uklad uproszczony szeregowy opor zastepczy

Rys. 4. Złożony układ szeregowo - równoległy z rysunku 3 można uprościć do połączenia szeregowego

Rozważmy układ elektrocznicny jak na rysunku 3. Pary oporników R1 i R2 oraz R3 i R4 są połączone równolegle. Możemy dla nich policzyć opory zastępcze zgodnie ze wzorem 2:

$${ \frac {1}{R_{1,2}} = \frac {1}{R_1}+\frac {1}{R_2} = \frac {1}{5000}+\frac {1}{10000} = \frac {3}{10000} }$$

$${ R_{1,2} = \frac {10000}{3} = 3333 (\Omega) }$$

$${ \frac {1}{R_{3,4}} = \frac {1}{R_3}+\frac {1}{R_4} = \frac {1}{1000}+\frac {1}{500} = \frac {3}{1000} }$$

$${ R_{3,4} = \frac {1000}{3} = 333 (\Omega) }$$ Uproszczony układ przedstawiono na rysunku 4. Widzimy na nim cztery oporniki połączone szeregowo - dwie pary oporników połączonych równolegle zastąpiono pojedynczymi rezystorami. W kolejnym kroku możemy więc obliczyć opór zastępczy korzystając ze wzoru 1:

$${ R = R_{1,2}+R_{3,4}+R_5+R_6 = 3333+333+4700+1000 }$$

$${ R = 9366 \Omega \approx 9,4 (k\Omega) }$$

Ostatecznie złożony układ oporników z rysunku 3. możemy zastąpić pojedynczym rezystorem o wartości 9,4 kΩ. Zauważmy, że zarówno ten przykład obliczeniowy, jak i przykłady najczęściej rozważane w edukacji, mają po dwa zaciski. W elektronice jednak nie zawsze tak jest. Stosuje się również układy o trzech i więcej zaciskach. W kolejnych paragrafach przedstawiono rozważania dotyczące transformacji układów trójzaciskowych – trójkąta i gwiazdy.

Przykład oporu zastępczego: transfiguracja trójkąt - gwiazda

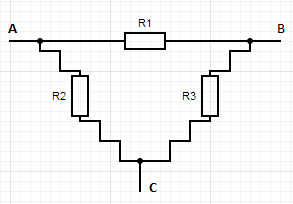Rys. 5. Oporniki połączone w układ trójkątny

Rys. 6. Oporniki połączone w układ gwiazdy

opor zastepczy transfiguracja trojkat gwiazda

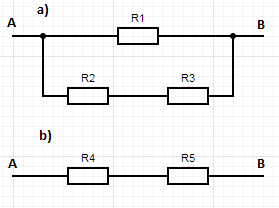Rys. 7. Uproszczone schematy układów do wyznaczenia oporów zastępczych - drogi przepływu prądu między zaciskami A i B w przypadku a) trójkąta b) gwiazdy

Wyobraźmy sobie, że mamy trzy oporniki połączone ze sobą w układzie trójkątnym (rysunek 5.). Układ ten chcemy zastąpić trzema opornikami połączonymi w gwiazdę (rysunek 6.). Oznacza to, że na wyjściach gwiazdy chcemy otrzymać takie same napięcia i prądy, jak na wyjściach trójkąta. Naszym zadaniem jest więc wyznaczenie oporów zastępczych między odpowiadającymi sobie zaciskami i porównanie ich. Weźmy na początek pod uwagę jedynie zaciski A i B. Prąd między tymi punktami może przepływać w przypadku trójkąta przez opornik R1 lub przez oporniki R2 i R3. W przypadku gwiazdy jedyna droga wiedzie przez R4 i R5. Dobrze obrazują tę sytuację schematy na rysunku 7. W obu przypadkach możemy zapisać opory zastępcze R_AB:

Opór zastępczy R_AB dla układu gwiazdy:

$${ \frac {1}{R_{AB}}=\frac{1}{R_1}+\frac{1}{R_2+R_3} \;>>\; R_{AB}=\frac{R_1(R_2+R_3)}{R_1+R_2+R_3} }$$

Opór zastępczy R_AB dla układu trójkątnego: $${ R_{AB}=R_4+R_5 }$$ Chcemy zastąpić jeden układ drugim, a więc opory pomiędzy poszczególnymi zaciskami (wyznaczone opory zastępczy) muszą być sobie równe:

$${ R_4+R_5=\frac{R_1(R_2+R_3)}{R_1+R_2+R_3} }$$

Takie samo rozumowanie przeprowadzamy dla zacisków A i C oraz B i C, stosując odpowiednie, wyznaczone opory zastępcze. Otrzymujemy układ równań: $${ R_4+R_5=\frac{R_1(R_2+R_3)}{R_1+R_2+R_3} \tag{3}}$$ $${ R_4+R_6=\frac{R_2(R_1+R_3)}{R_1+R_2+R_3} \tag{4}}$$ $${ R_5+R_6=\frac{R_3(R_1+R_2)}{R_1+R_2+R_3} \tag{5}}$$ Układ ten rozwiążemy metodą podstawiania. Z równania 6 wyznaczamy opór R6. Jednocześnie wymnażamy wyrażenie w liczniku: $${ R_6=\frac{R_1R_3+R_2R_3}{R_1+R_2+R_3} - R_5 }$$ Podstawiamy rezystancję R6 do równania 4. Jednocześnie wyznaczamy wartość oporu R5:

$${ R_4+\frac{R_1R_3+R_2R_3}{R_1+R_2+R_3} - R_5=\frac{R_1R_2+R_2R_3}{R_1+R_2+R_3} }$$

$${ R_5=R_4 + \frac{R_1R_3+R_2R_3-R_1R_2-R_2R_3}{R_1+R_2+R_3} }$$ Wyznaczony opór R5 podstawiamy do równania 3. Wyznaczamy rezystancję R4:

$${ R_4+R_4 + \frac{R_1R_3+R_2R_3-R_1R_2-R_2R_3}{R_1+R_2+R_3}=\frac{R_1R_2+R_1R_3}{R_1+R_2+R_3} }$$

$${ 2R_4 =\frac{R_1R_2+R_1R_3-R_1R_3-R_2R_3+R_1R_2+R_2R_3}{R_1+R_2+R_3} }$$

$${ R_4 =\frac{R_1R_2}{R_1+R_2+R_3} }$$ Analogiczną procedurę można przeprowadzić dla rezystancji R5 i R6. Ostatecznie otrzymamy wartości: $${ R_4 =\frac{R_1R_2}{R_1+R_2+R_3} \tag{6}}$$ $${ R_5 =\frac{R_1R_3}{R_1+R_2+R_3} \tag{7}}$$ $${ R_6 =\frac{R_2R_3}{R_1+R_2+R_3} \tag{8}}$$ Tym sposobem wyznaczyliśmy wzory na transfigurację trójkąt - gwiazda (wzory 6, 7 i 8) stosując poznane wcześniej metody obliczania oporów zastępczych dla układu szeregowego i równoległego.

Przykład oporu zastępczego: transfiguracja gwiazda - trójkąt

Można również przeprowadzić transformację w drugą stronę, to jest z układu gwiazdy otrzymać układ trójkątny. Rozumowanie jest analogiczne jak w przypadku transformacji trójkąt – gwiazda. W szczególności stosujemy te same porównania wyznaczonych oporów zastępczych między odpowiadającymi sobie zaciskami. Można więc skorzystać z tych samych równań. Najwygodniej jest zacząć od wyników końcowych obliczeń (równania 6, 7 i 8): $${ R_4 =\frac{R_1R_2}{R_1+R_2+R_3} \tag{9}}$$ $${ R_5 =\frac{R_1R_3}{R_1+R_2+R_3} \tag{10}}$$ $${ R_6 =\frac{R_2R_3}{R_1+R_2+R_3} \tag{11}}$$ Wyznaczenie z tego układu oporów R1, R2 i R3 metodą podstawiania będze bardzo pracochłonne, gdyż są one uwikłane w skomplikowane ułamki. Możemy jednak „sprytnie” przemnożyć równania 1 i 2, 1 i 3 oraz 2 i 3 przez siebie. Otrzymamy: $${ R_4 R_5 =\frac{R_1^{2}R_2R_3}{(R_1+R_2+R_3)^{2}} }$$ $${ R_4 R_6 =\frac{R_1R_2^{2}R_3}{(R_1+R_2+R_3)^{2}} }$$ $${ R_5 R_6 =\frac{R_1R_2R_3^{2}}{(R_1+R_2+R_3)^{2}} }$$ A następnie dodać powyższe stronami:

$${ R_4R_5 + R_4R_6 + R_5R_6 = \frac{R_1^{2}R_2R_3+R_1R_2^{2}R_3+R_1R_2R_3^{2}}{(R_1+R_2+R_3)^{2}} = \frac {R_1R_2R_3}{R_1+R_2+R_3} }$$

Podzielmy teraz to równanie stronami kolejno przez równania 9, 10 i 11:

$${ \frac{R_4R_5 + R_4R_6 + R_5R_6}{R_4} = \frac {R_1R_2R_3}{R_1+R_2+R_3} \cdot \frac{R_1+R_2+R_3}{R_1R_2} }$$

$${ \frac{R_4R_5 + R_4R_6 + R_5R_6}{R_5} = \frac {R_1R_2R_3}{R_1+R_2+R_3} \cdot \frac{R_1+R_2+R_3}{R_1R_3} }$$

$${ \frac{R_4R_5 + R_4R_6 + R_5R_6}{R_6} = \frac {R_1R_2R_3}{R_1+R_2+R_3} \cdot \frac{R_1+R_2+R_3}{R_2R_3} }$$

Z prawych stron równania rezystancje w ułamkach się skracają. Po uproszczeniu otrzymujemy szukane wartości oporów R1, R2 i R3: $${ R_3 = R_5 + R_6 + \frac{R_5R_6}{R_4} \tag{12}}$$ $${ R_2 = R_4 + R_6 + \frac{R_4R_6}{R_5} \tag{13}}$$ $${ R_1 = R_4 + R_5 + \frac{R_4R_5}{R_6} \tag{14}}$$ Tym sposobem otrzymaliśmy wzory na transfigurację gwiazda - trójkąt (wzory 12, 13 i 14) poprzez zastosowanie wzorów na opory zastępcze dla układów szeregowego i równoległego.
Powyższe transformacje (w postaci gotowych równań 6, 7 i 8 oraz 12, 13 i 14) są bardzo przydatnym narzędziem w elektronice. W niektórych złożonych układach nie da się policzyć oporu zastępczego wprost ze wzorów 1 i 2, gdyż połączenia oporników nie są szeregowe ani równoległe, ale występuje właśnie układ z trzema zaciskami. Oprócz trójników (trzy zaciski) w elektronice często rozważa się również czwórniki (cztery zaciski).

Układ zastępczy opornika, cewki, kondensatora [1]

Rys. 8. Schemat zastępczy rzeczywistego opornika. Przy bardzo dokładnych obliczeniach należy uwzględnić nie tylko rezystancję, ale też indukcyjność i pojemność elektryczną rezystora

Na koniec jeszcze raz zwróćmy uwagę, że nie tylko oporniki posiadają rezystancję. Proste przypisanie opornik – rezystancja, cewka – indukcyjność, kondensator – pojemność elektryczna jest uproszczeniem. Taki model dobrze sprawdza się w układach z prądem stałym lub o niskiej częstotliwości oraz w obliczeniach szacunkowych. Rzeczywista cewka i kondensator są przecież wykonane z metali o pewnych określonych oporach właściwych. Cewka wykazuje również pewną niewielką pojemność elektryczną. Podobnie w oporniku w obwodzie prądu przemiennego indukuje się niewielki prąd samoindukcji. Przykładowo na rysunku 8 przedstawiony jest układ zastępczy rzeczywistego opornika.

Szybki teścik

Bibliografia

Elementy elektryczne układów elektronicznych, http://www.zstio-elektronika.pl/pliki_zsz/PEiE-Elementy_elektryczne_ukladow_elektroniczynch.pdf, dostęp: 11.01.2022