02.01.2023r
Metoda Najmniejszych Kwadratów (MNK) w fizyce
Spis treści- Kiedy stosujemy Metodę Najmniejszych Kwadratów w fizyce? (Ś)
- Eksperyment fizyczny z Metodą Najmniejszych Kwadratów (Ś)
- MNK od strony matematycznej (T)
- MNK w praktyce (Ś)
- Fizyka w arkuszu kalkulacyjnym - Metoda Najmniejszych Kwadratów (Ś)
- Metoda Najmniejszych kwadratów dla nieliniowych wielkości fizycznych (T)
- Znam podstawy Metody Najmniejszych Kwadratów – co dalej? (T)
- Zadanie na MNK – próbka zanieczyszczona radionuklidem (T)
Głównym źródłem wiedzy w fizyce jak i innych naukach przyrodniczych, obok wyników wnioskowania teoretycznego z aktualnej wiedzy o świecie, jest eksperyment. W doświadczeniach fizycznych czasem wystarcza wykonać pojedynczy pomiar, aby uzyskać wartościowe informacje o danym przedmiocie badania. Tak jest np. gdy mierzymy nasz wzrost centymetrem krawieckim lub masę stając na wadze łazienkowej. Gdy zależy nam jednak na dokładności wyniku, i chcemy zminimalizować niepewność pomiaru, najlepiej jest wykonać całą serię pomiarową. Do jej analizy z kolei najlepiej jest zastosować Metodę Najmniejszych Kwadratów.
Kiedy stosujemy Metodę Najmniejszych Kwadratów w fizyce?
Wyobraźmy sobie, że mamy w laboratorium opornik o nieznanej oporności i chcemy go zbadać – uzyskać informacje o jego rezystancji. Znając prawo Ohma: $${ I = \frac{1}{R} U }$$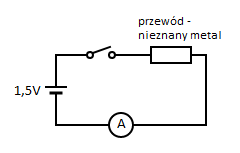
Rys. 1. Schemat prostego układu do weryfikacji prawa Ohma Metodą Najmniejszych Kwadratów.
Inaczej rzecz się ma w przypadku, gdy jakąś wielkość fizyczną chcemy zmierzyć tylko w jednym, konkretnym punkcie. Dobrym przykładem jest pomiar masy ciała. W tym przypadku również wykonanie kilku pomiarów pozwoli uzyskać dokładniejszy wynik, mniejszą niepewność, niż wykonanie jednego pomiaru. Tutaj jednak ostatecznym wynikiem eksperymentu będzie średnia z serii pomiarowej, a niepewnością pomiaru – odchylenie standardowe średniej. W tym przypadku nie zastosujemy Metody Najmniejszych Kwadratów, gdyż masa danego człowieka ma zawsze tę samą wartość, a jedynie wynik będzie fluktuował wokół średniej (więcej na temat pomiarów w eksperymencie z masą można znaleźć na stronie poświęconej niepewnościom pomiarowym).
Eksperyment fizyczny z Metodą Najmniejszych Kwadratów
Załóżmy, że wyznaczamy opór elektryczny przewodu metalowego, ale nie mamy pewności, czy spełnia on prawo Ohma (czy jego opór jest stały). W takim przypadku składamy układ pomiarowy jak na schemacie (Rys. 1.).Jako źródło napięcia stosujemy typową baterię AA o napięciu 1,5V, nie musimy więc wykonywać pomiarów napięcia, a jedynie natężenia prądu. Po wykonaniu pomiaru dołączamy szeregowo drugą, trzecią i czwartą baterię uzyskując serię pomiarową (rysunek 2.):

Rys. 2. Tabela z wynikami napięcia i natężenia prądu. Regresja liniowa będzie możliwa, jeżeli punkty pomiarowe utworzą linię prostą na wykresie.
Następnie nanosimy punkty pomiarowe na wykres (Rys. 3.):

Rys. 3. Wykres zależności natężenia prądu od napięcia. Punkty pomiarowe układają się na linii prostej, możemy więc przeprowadzić regresję liniową Metodą Najmniejszych Kwadratów.
Metoda Najmniejszych Kwadratów od strony matematycznej
Stwierdziliśmy, że prawo Ohma jest spełnione, więc natężenie prądu zależy liniowo od napięcia: $${ I = \frac{1}{R} U \tag{1} }$$ Punkty zaś układają się na prostej, którą możemy opisać funkcją liniową postaci: $${ y=ax ~ + ~ b \tag{2} }$$ Metoda Najmniejszych Kwadratów polega na wybraniu prostej (co rozumiemy jako znalezienie współczynników a i b funkcji liniowej) najlepiej dopasowanej do uzyskanych punktów (regresja liniowa). Wtedy będziemy mogli stwierdzić, że opór elektryczny zależy od uzyskanego z regresji liniowej współczynnika kierunkowego prostej (na podstawie porównania wzorów 1 i 2): $${ R = \frac{1}{a} }$$ Dla każdego punktu pomiarowego występuje pewna niewielka różnica między wartością w punkcie, a wartością jaka wynikałaby z przyjętej funkcji liniowej:$${ \Delta i = y_{i} ~ – ~ f(x_{i}) = y_{i} – (ax_{i}+b) }$$
Miarą dobroci dopasowania funkcji w Metodzie Najmniejszych Kwadratów będzie suma kwadratów tych różnic dla wszystkich n punktów:
$${ \chi ^{2} (a, b) = \sum^{n}_{i} (y_{i}-(f(x_{i})))^{2} = \sum^{n}_{i} (y_{i}-(ax_{i}+b))^{2} \tag{3} }$$
Najlepsza funkcja to ta, dla której suma kwadratów różnic - Chi2 - jest najmniejsza:
$${ \chi ^{2}(a, b) = min }$$
Z analizy matematycznej wiemy, że funkcja przyjmuje wartość najmniejsza, gdy pochodna wynosi 0:
$${ \frac{d(\chi ^{2}(a,b))}{da} = 0 ~~~~ oraz ~~~~ \frac{d(\chi ^{2}(a,b))}{db} = 0 }$$
$${ \frac{d(\sum^{n}_{i} (y_{i}-(ax_{i}+b))^{2})}{da} = 0 ~~~~ oraz ~~~~ \frac{d(\sum^{n}_{i} (y_{i}-(ax_{i}+b))^{2})}{db} = 0 }$$
Dalej prowadzimy obliczenia dla pochodnej po współczynniku kierunkowym a:
$${ 0 ~ = ~ \frac{d(\sum^{n}_{i} (y_{i}-(ax_{i}+b))^{2})}{da} = \sum^{n}_{i} 2(y_{i}-(ax_{i}+b)) \cdot (-x_{i}) = 2 ~ \sum^{n}_{i} (-x_{i}y_{i} + ax^{2}_{i} +bx_{i} ) }$$
$${ 0 ~ = ~ - \sum^{n}_{i} (x_{i}y_{i}) + a \sum^{n}_{i} x^{2}_{i} + b \sum^{n}_{i} x_{i} \tag{4} }$$
a następnie obliczenia dla pochodnej po wyrazie wolnym b:
$${ 0 ~ = ~ \frac{d(\sum^{n}_{i} (y_{i}-(ax_{i}+b))^{2})}{db} = \sum^{n}_{i} 2(y_{i}-(ax_{i}+b)) \cdot (-1) = 2 ~ \sum^{n}_{i} (-y_{i} + ax_{i} + b ) }$$
$${ 0 ~ = ~ - \sum^{n}_{i} y_{i} + a\sum^{n}_{i} x_{i} + b n }$$
$${ b ~ = ~ \frac{1}{n} ( \sum^{n}_{i} y_{i} - a\sum^{n}_{i} x_{i} ) \tag{5} }$$
Następnie podstawiamy b z równania 5. do równania 4. :
$${ 0 ~ = ~ - \sum^{n}_{i} (x_{i}y_{i}) + a \sum^{n}_{i} x^{2}_{i} + \frac{1}{n} ( \sum^{n}_{i} y_{i} - a\sum^{n}_{i} x_{i} ) \sum^{n}_{i} x_{i} ~ = ~ - \sum^{n}_{i} (x_{i}y_{i}) + a \sum^{n}_{i} x^{2}_{i} + \frac{1}{n} \sum^{n}_{i} (x_{i}y_{i}) - a \frac{1}{n} \sum^{n}_{i} x^{2}_{i} }$$
oraz wyznaczamy współczynnik a najlepiej dopasowanej funkcji liniowej wg Metody Najmniejszych Kwadratów:
$${ a ~ = ~ \frac{ \sum^{n}_{i} (x_{i}y_{i}) - \frac{1}{n} \sum^{n}_{i} (x_{i}y_{i}) }{ \sum^{n}_{i} x^{2}_{i} - \frac{1}{n} \sum^{n}_{i} x^{2}_{i} } ~ = ~ \frac{ n \sum^{n}_{i} (x_{i}y_{i}) - \sum^{n}_{i} (x_{i}y_{i}) }{ n \sum^{n}_{i} x^{2}_{i} - \sum^{n}_{i} x^{2}_{i} } }$$
Dzięki tej długiej serii przekształceń równań, otrzymujemy bardzo proste i użyteczne wzory na współczynnik kierunkowy a oraz wyraz wolny b funkcji liniowej, która jest najlepiej dopasowana do danych pomiarowych!:
$${ a ~ = ~ \frac{ n \sum^{n}_{i} (x_{i}y_{i}) - \sum^{n}_{i} (x_{i}y_{i}) }{ n \sum^{n}_{i} x^{2}_{i} - \sum^{n}_{i} x^{2}_{i} } \tag{6} }$$
$${ b ~ = ~ \frac{1}{n} ( \sum^{n}_{i} y_{i} - a\sum^{n}_{i} x_{i} ) \tag{7} }$$
Podsumowując, Metoda Najmniejszych Kwadratów pozwala w prosty sposób otrzymać współczynniki a i b funkcji liniowej najlepiej dopasowanej do naszych danych eksperymentalnych. Wystarczy, że w tym celu skorzystamy z gotowych wzorów 6 i 7. Następnie współczynniki a i b wykorzystujemy do policzenia wartości interesujących nas wielkości fizycznych. W przypadku eksperymentu z prawem Ohma:
$${ R = \frac{1}{a} }$$
$${ b \approx 0 ~~ (bo ~ współczynnik ~ b ~ nie ~ występuje ~ w ~ prawie ~ Ohma) }$$
Metoda Najmniejszych Kwadratów w praktyce
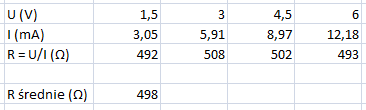
Rys. 4. Wartości rezysjancji dla policzone dla każdego z punktów oddzielnie, oraz wartrość średnia oporu.
Otrzymana wartość średnia rezystancji wynosi 498 Ω - jest to opór metalu, z którego wykonano nieznany przewód.
Teraz obliczmy opór stosując regresję liniową Metodą Najmniejszych Kwadratów. W tym celu policzymy współczynniki kierunkowy a i wolny b ze wzorów 6 i 7 - rysunek 5.
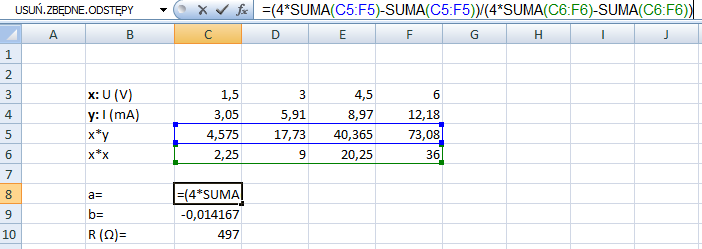
Rys. 5. Obliczenia wartości oporu w eksperymencie fizycznym Metodą Najmniejszych Kwadratów w programie excel. Wartość wyrazu wolnego b jest bliska 0 - jest to zgodne z oczekiwaniem, gdyż wyraz wolny nie występuje w prawie Ohma (patrz wzór 1.).
Jak widzimy, rezystancja policzona Metodą Najmniejszych Kwadratów wynosi 497 Ω, a więc nieznacznie mniej niż wartość średnia z punktów. Jako wartość bardziej wiarygodną należy traktować właśnie wartość otrzymaną w wyniku regresji liniowej - jest to ściśle zbadana i powszechnie stosowana metoda badawcza na całym świecie.
Fizyka w arkuszu kalkulacyjnym - Metoda Najmniejszych Kwadratów
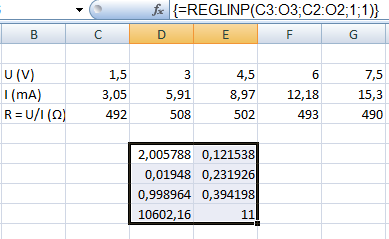
Rys. 6. Wbucowana funkcja REGLINP w programie Excel umożliwiająca szybkie policzenie regresji liniowej Metodą Najmniejszych Kwadratów.
Funkcja ta zwraca tablicę 2x5 wartości. Najbardziej interesujące są dwa pierwsze wiersze - pierwsza kolumna opisuje współczynnik kierunkowy a, a druga wyraz wolny b. Znaczenie pozostałych wartości można znaleźć na stronie Microsoftu.
W przypadku, gdy nie mamy na swoim komputerze pakietu Microsoft Office, polecam zainstalowanie programu Gumeric, który jest darmowym odpowiednikiem Excela i jest dostępny zarówno na systemie Windows jak i Linux. W Gnumericu odpowiednikiem funkcji REGLINP jest LINEST.
Zastosujmy nowo poznaną funkcję do policzenia Metodą Najmniejszych Kwadratów rezystancji naszego przewodu. Tym razem dodamy jednak więcej punktów pomiarowych - sprawdźmy co dzieje się z przewodem po podłączeniu wyższych napięć. Zastępujemy baterie zasilaczem - nadal jednak zmieniamy napięcia co 1,5 V. Wyniki przedstawia tabela na rysunku 7.

Rys. 7. Tabela wyników pomiarów napięcia i natężenia prądu - weryfikacja prawa Ohma Metodą Najmniejszych Kwadratów.
Serię pomiarową wyników odkładamy na wykresie zależności natężenia prądu od przyłożonego napięcia - rysunek 8.
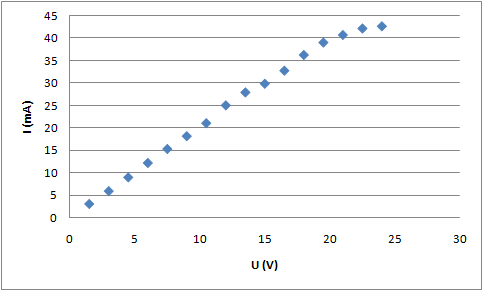
Rys. 8. Wykres zależności natężenia prądu od przyłożonego napięcia. Jak widać, trzy ostatnie punkty pomiarowe nieco odbiegają od linii prostej.
Jak widać na wykresie na rysunku 8., ostatnie trzy punkty zaczynają odstawać od linii prostej. Może dla wyższych napięc metal nabiera nowych właściwości? Może jest to efekt nagrzania się układu pomiarowego? Zaobserwowaliśmy moment, w którym prawo Ohma przestaje być spełnione. Nadal jednak możemy przeprowadzić regresję liniową Metodą Najmniejszych Kwadratów. Unikniemy błędu, jeśli z regresji wyrzucimy trzy ostatnie, odstające od linii prostej punkty.

Rys. 9. Opór elektryczny przewodnika policzony Metodą Najmniejszych Kwadratów poprzez zastosowanie funkcji REGLINP w Excelu.
Stosując Metodę Najmniejszych Kwadratów otrzymaliśmy wartość rezystancji równą 499 Ω. Na koniec zobaczmy jeszcze, jak otrzymana w wyniku regresji liniowej prosta układa się na wykresie. W tym celu nanosimy na wykres z rysunku 8. prostą o równaniu f(U) = ax+b - rys. 10.

Rys. 10. Wykres zależności natężenia prądu od przyłożonego napięcia wraz z nałożoną prostą najlepszego dopasowania otrzymaną Metodą Najmniejszych Kwadratów.
Jak widać istnienie gotowych formuł w arkuszach kalkulacyjnych bardzo upraszcza stosowanie Metody Najmniejszych Kwadratów i zapewnia jej powszechność bez potrzeby znania wyższej matematyki.
Metoda Najmniejszych kwadratów dla nieliniowych wielkości fizycznych
Zarówno przytoczony przykład eksperymentu fizycznego z prawem Ohma, jak i wyprowadzone wzory w akapicie „Metoda Najmniejszych Kwadratów od strony matematycznej” dotyczyły zależności liniowych. Również formuły arkuszów kalkulacyjnych obsługują Metodę Najmniejszych Kwadratów tylko dla funkcji liniowych (sugerują to z resztą nazwy funkcji: REGresjaLINiowaP i LINEST). Co zrobić gdy wielkość fizyczna opisana jest zależnością nie liniową, lecz kwadratową lub logarytmiczną?Pierwszym sposobem jest wyznaczenie wzorów od początku, „na piechotę”. Zauważmy, że wzór 3 jest ogólny i możemy do niego podstawić nie tylko funkcję liniową, ale też np. logarytmiczną:
$${ \chi^{2}(a, b) ~ = ~ \sum^{n}_{i} (y_{i}-(f(x_{i})))^{2} ~ = ~ \sum^{n}_{i} (y_{i}-(a ~ ln(x_{i}) + b))^{2} }$$
Następnie, podobnie jak w przypadku funkcji liniowej, liczymy pochodną i przyrównujemy ją do 0. W ten sposób otrzymamy nowy wzór na szukany współczynnik.Takie zastosowanie Metody Najmniejszych Kwadratów ma jednak wady. Po pierwsze wyznaczenie współczynników w przypadku skomplikowanych funkcji może być trudne. Po drugie nie ma gotowych funkcji w excelu czy gnumericu do dopasowania funkcji nieliniowych.
Drugim sposobem jest linearyzacja zależności, a następnie dopasowanie do danych fizycznych funkcji liniowej. Na czym polega „linearyzacja”?
Wróćmy do opisanego wcześniej przykładu funkcji logarytmicznej: y=a ln(x) + b
Zmienna y jest zależna od x w sposób logarytmiczny. Możemy też jednak powiedzieć, że y jest zależny liniowo od ln(x). Oznacza to, że nanoszone punkty (ln(x), y) na wykresie ułożą się na linii prostej (Rys. 11). Zastosowanie Metody Najmniejszych Kwadratów poprzez funkcję REGLINP do tak przetworzonych danych pozwala na poprawne wyznaczenie współczynnika kierunkowego a i wyrazu wolnego b.

Rys. 11. Metoda Najmniejszych Kwadratów dla przykładowej zależności nieliniowej. Funkcji Excelowej REGLINP możemy użyć do przeprowadzenia regresji po uprzednim zlinearyzowaniu funkcji.
Jak widzimy na rysunku, stosując formułę REGLINP otrzymaliśmy następujące wartości współczynników: a = 5, b = 4. Możemy więc teraz stwierdzić, że dane eksperymentalne (z tabeli na rysunku 11.), o których wiedzieliśmy, że zależą od siebie w sposób logarytmiczny, spełniają zależność: $${ y ~ = ~ 5 ~ ln(x) ~ + ~ 4 }$$ Jak więc pokazaliśmy na prostym przykładzie, możemy stosować funkcję REGLINP do przeprowadzania regresji Metodą Najmnijeszych Kwadratów również w przypadku zależności nieliniowych, o ile tylko wiemy, w jaki sposób zależność tę zlinearyzować. Tam, gdzie linearyzacja jest możliwa, jest to metoda szybsza i prostsza niż opisana wcześniej metoda analityczna.
Znam podstawy Metody Najmniejszych Kwadratów – co dalej?
Powyżej opisana została najbardziej praktyczna od strony opracowywania danych eksperymentalnych w fizyce część Metody Najmniejszych Kwadratów. Dodatkowo warto wiedzieć, że:- Współczynniki prostej (ew. innej krzywej) są wyznaczane z niepewnościami, wartość niepewności również można obliczyć – zwraca je również funkcja REGLINP i LINEST w drugim wierszu omawianej tabelki 2x5.
- Pomiary fizyczne zawsze obarczone są niepewnościami. W przypadku, gdy niepewności znacząco się różnią dla różnych punktów pomiarowych, należy je również uwzględnić w regresji Metodą Najmniejszych Kwadratów. W praktyce oznacza to, że punkty pomiarowe o większej niepewności mają mniejszy wpływ na dopasowywana prostą niż punkty określone z mniejszą niepewnością.
Zadanie na MNK – próbka zanieczyszczona radionuklidem
Do laboratorium trafiła próbka ziemi zanieczyszczona nieznanym radionuklidem. Przez 5 dni, codziennie o 12:00, badano aktywność próbki. Wyniki przedstawia tabela:
- Narysuj wykres aktywności próbki od czasu A(t)
- Narysuj wykres zlinearyzowany
- Wyznacz stałą rozpadu izotopu korzystając z Metody Najmniejszych Kwadratów
- Oblicz okres połowicznego zaniku izotopu. Czy tym izotopem może być jod I-131?

