17.03.2022r
Prawo Ohma
Spis treści- Zarys historyczny (Ł)
- Czym jest opór elektryczny? (Ł)
- Pomiar oporu opornika (Ł)
- Inne metody pomiaru oporu elektrycznego (Ś)
- Opór właściwy (Ł)
- Ograniczenia dla prawa Ohma (Ś)
- Dzielnik napięcia (Ś)
- Szybki teścik
Zarys historyczny

Rys. 1. Georg Simon Ohm, niemiecki fizyk i matematyk. Żył w latach 1789 –1856 [1]
Georg Simon Ohm (rys. 1.) wykonał wspomniane doświadczenie w 1825 roku. Zaobserwował, że natężenie prądu przepływającego w przewodniku jest proporcjonalne do przyłożonego napięcia, co symbolicznie zapisujemy:
$$ {I=\frac{1}{R} U} \tag{1} $$ Z czasem odkryto szereg dodatkowych uwarunkowań i ograniczeń, czego nie można było stwierdzić z pierwotnego doświadczenia.
Czym jest opór elektryczny?
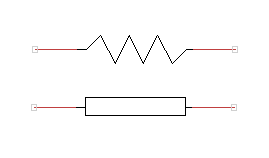
Oporność elektryczna jest właściwością materii, możemy więc ją przypisać wszystkim ciałom, podobnie jak każde ciało ma swoją masę i temperaturę. Przykładowo, oporność metalowego pręta będzie równa ułamkowi oma, podczas gdy oporność ciała człowieka jest rzędu megaomów. W elektronice mówimy o oporności poszczególnych praktycznych elementów elektronicznych, takich jak źródło napięcia (bateria), żarówka, cewka, przewód. Mamy też jednak szczególny element – opornik (rezystor) – którego jedyną cechą jest właśnie posiadanie oporu elektrycznego o określonej wartości (po co „dokładać” do obwodu coś, co utrudnia przepływ prądu i nic poza tym nie robi? Przykład w akapicie „dzielnik napięcia”). Na rysunku 2 przedstawiono przykładowe oporniki oraz symbole stosowane w schematach elektronicznych.
a)

b)
c)
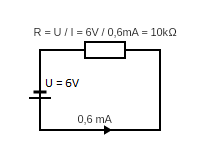 Rys. 3. Praktyczne wykorzystanie prawa Ohma do wyliczenia oporu
Rys. 3. Praktyczne wykorzystanie prawa Ohma do wyliczenia oporu
Pomiar oporu opornika
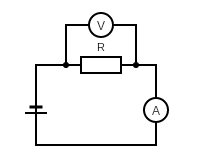 Rys. 4. Schemat do pomiaru oporu elektrycznego woltomierzem i amperomierzem
Rys. 4. Schemat do pomiaru oporu elektrycznego woltomierzem i amperomierzem
Inne metody pomiaru oporu elektrycznego
-
Poprzez poprawny pomiar natężenia i napięcia
Zauważmy, że pomiar opisany w poprzednim akapicie ma tę wadę, że amperomierz mierzy prąd płynący nie tylko przez opornik, ale też przez woltomierz (jest to mały prąd, ale jednak!). Udoskonaleniem metody będzie oddzielne zmierzenie napięcia i natężenia prądu w układach jak na schematach na rysunku 5.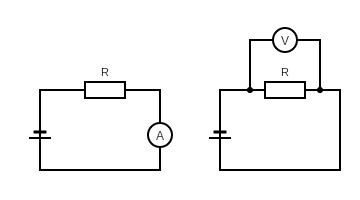 Rys. 5. Układy poprawnego mierzenia natężenia i napięcia
Rys. 5. Układy poprawnego mierzenia natężenia i napięcia
-
Seria pomiarowa
Chcąc uzyskać dokładny wynik, dobry eksperymentator często wykonuje całą serię pomiarów (zazwyczaj powyżej 10), dla różnych wartości przyłożonego napięcia. Dzięki takiemu podejściu minimalizuje się błąd statystyczny, a jednocześnie można wychwycić błędy grube. Uzyskane punkty pomiarowe należy odłożyć na wykresie I(U), a następnie poprowadzić linię najlepszego dopasowania metodą „na oko” (mniej profesjonalnie) lub Metodą Najmniejszych Kwadratów (bardzo profesjonalnie) – rys. 6.Zauważmy, że taka prosta jest nachylona pod pewnym kątem alfa do osi x. Z matematyki wiemy, że tangens tego kąta jest równy współczynnikowi kierunkowemu funkcji liniowej: $$ {tg(\alpha)=a} $$ a zgodnie ze wzorem (1) (prawo Ohma jest de facto funkcją liniową)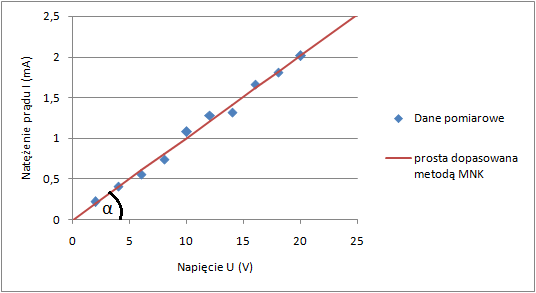
Rys. 6. Wyznaczenie rezystancji opornika metodą MNK
$$ {a=\frac{1}{R}} $$ stąd:
$$ {R=\frac{1}{a}} $$ Więcej szczegółów dotyczących tej metody znajduje się w temacie Metoda Najmniejszych Kwadratów. -
Metoda porównawcza
Najdokładniejsze pomiary rezystancji uzyskuje się metodą porównawczą. W tej metodzie opornik o nieznanej rezystancji porównuje się z drugim, znanym i dobrze określonym opornikiem. Schemat układu przedstawiono na rysunku 7. Rys. 7. Układ do mierzenia rezystancji metodą porównawczą. Niezbędne jest stabilne źródło prądowe i woltomierz wysokiej klasy
Rys. 7. Układ do mierzenia rezystancji metodą porównawczą. Niezbędne jest stabilne źródło prądowe i woltomierz wysokiej klasy
W układzie złożonym z dwóch szeregowo połączonych oporników oraz źródła napięcia płynie prąd o natężeniu I. Mierzymy kolejno napięcia na jednym i drugim oporniku tym samym woltomierzem.
$$ {R_1=\frac{U_1}{I}} $$ $$ {R_x=\frac{U_x}{I}} $$ $$ {R_x=\frac{U_1}{U_x R_1}} $$ Zauważmy, że w metodzie tej nie musimy znać natężenia prądu I. Dodatkowo błędy pomiaru napięć częściowo się kompensują, co dodatkowo zwiększa dokładność oszacowania (woltomierz może mieć błąd systematyczny, jednak będzie on podobny w obu pomiarach).
Wybór metody pomiaru zależy od eksperymentu. Nie zawsze dokładność jest najważniejsza, czasem lepiej zastosować metodę szybszą lub tańszą.
Opór właściwy
Wyobraźmy sobie, że do połączenia obwodu jak na rysunku 3 zużyto 2 m przewodu miedzianego o przekroju 0,75mm^2. Jak policzyć opór takiego przewodu? Czy jest on duży w porównaniu do oporu opornika?Aby to stwierdzić, należy posłużyć się oporem właściwym materiału, który należy rozumieć jako opór elektryczny, jaki stawia element wykonany z tego materiału o długości jednostkowej (1m) oraz przekroju jednostkowym (a więc 1m^2). Przykładowe oporności przedstawia poniższa tabela:
Tabela 1. Wybrane materiały i ich opory właściwe [4]
| $$ {Materiał} $$ | $$ {Opór \; właściwy \; \rho \;(\Omega m)} $$ |
| srebro | $$ {1,6\cdot 10^{-8}} $$ |
| miedź | $$ {1,7\cdot 10^{-8}} $$ |
| glin | $$ {2,8\cdot 10^{-8}} $$ |
| wolfram | $$ {5,3\cdot 10^{-8}} $$ |
| platyna | $$ {1,1\cdot 10^{-7}} $$ |
| krzem | $$ {2,5\cdot 10^{3}} $$ |
| szkło | $$ {10^{10} - 10^{14}} $$ |
$$ {R=\rho \frac{l}{S}} \tag{2}$$ A więc w naszym przypadku opór elektryczny zużytego przewodu wynosi:
$$ {R=1,7 \cdot 10^{-8} \cdot \frac{2}{0,75\cdot10^{-6}} = 0,045 (\Omega)} $$
Ograniczenia dla prawa Ohma
Prawo Ohma świetnie odwzorowuje przepływ prąd w standardowych obwodach elektrycznych i elektronicznych, przez co jest prostym i powszechnie stosowanym modelem. Istnieje jednak szereg uwarunkowań, w których model ten się nie sprawdza. Są to np.:- Duże wahania temperatur – wraz ze wzrostem temperatury, opór właściwy materiału (a więc i opór elementu) wzrasta w przybliżeniu liniowo
- Szczególny rodzaj materiałów – półprzewodniki, dla których opór elektryczny maleje ze wzrostem temperatury
- Szczególny rodzaj materiałów – nadprzewodniki. Dla bardzo niskiej temperatury, rzędu kilku, kilkudziesięciu kelwinów, opór elektryczny zanika.
- Prąd elektryczny przemienny – w przypadku prądu przemiennego prawo Ohma ma nieco inną postać. Po włączeniu do obwodu z prądem przemiennym kondensatora lub cewki, obserwuje się przesunięcie fazy napięcia i natężenia prądu. Odczytane wartości chwilowe napięcia i natężenia nie będą więc spełniać prawa Ohma. Możemy jednak śmiało stosować to prawo biorąc wartości maksymalne lub skuteczne 😊
Dzielnik napięcia
Na koniec pozostaje pytanie – po co włączać do układu element, który stanowi dodatkowy opór dla przepływającego prądu? Przecież dodatkowy opór generuje straty energii w postaci wydzielającego się ciepła. Rys. 8. Układ do mierzenia rezystancji metodą porównawczą. Niezbędne jest stabilne źródło prądowe i woltomierz wysokiej klasy
Rys. 8. Układ do mierzenia rezystancji metodą porównawczą. Niezbędne jest stabilne źródło prądowe i woltomierz wysokiej klasy
Dwa identyczne oporniki połączone są szeregowo do napięcia sieciowego, a więc napięcie na każdym z nich wynosi:
$$ {U_1=U_2= \frac{U}{2}=115V} $$ Żarówka połączona jest równolegle z opornikiem, a więc napięcie na niej również wynosi 115V. Dobierając oporniki o odpowiednim stosunku rezystancji jesteśmy w stanie uzyskać potrzebne nam napięcie.
Uwaga! Podany przykład jest poglądowy. W praktycznym zastosowaniu należy zwrócić uwagę również na natężenie prądu jakie uzyskamy na urządzeniu (może być zbyt duże w przypadku zbyt małej rezystancji lub zbyt małe, przy dużej), a co za tym idzie wydzielającej się mocy (istnieje niebezpieczeństwo przegrzania się układu).
Szybki teścik
Bibliografia
- Georg Ohm, https://pl.wikipedia.org/wiki/Georg_Ohm, dostęp: 22.12.2021
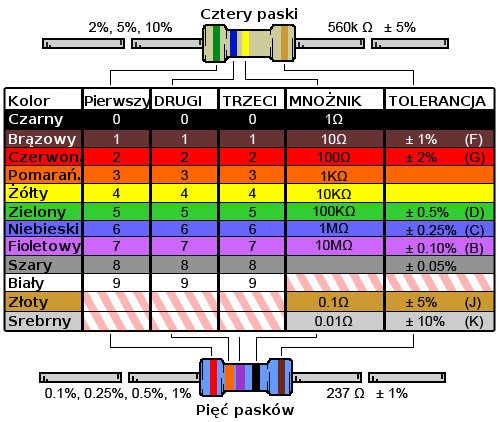
- Przykładowe oporniki, https://pl.wiktionary.org/wiki/opornik, dostęp: 22.12.2021
- Oznaczenia oporników, https://abc-rc.pl/product-pol-7053-Rezystor-0-25W-10K-100-szt-oporniki-rezystory-100szt.html, dostęp 22.12.2021
- Opór właściwy, tabela, https://home.agh.edu.pl/~kakol/efizyka/w21/main21b.html, dostęp: 22.12.2021

